دليل المبرمج لتجارب تعلم الآلة

جدول الروابط

نبذة مختصرة و 1. مقدمة

1.1 التفسير اللاحق

1.2 مشكلة الاختلاف

1.3 تشجيع توافق التفسير

1. الأعمال ذات الصلة

2. Pear: منظم اتفاق المفسر اللاحق

3. فعالية تدريب التوافق

   4.1 مقاييس الاتفاق

   4.2 تحسين مقاييس التوافق

   [4.3 الاتساق بأي ثمن؟]()

   4.4 هل التفسيرات لا تزال قيمة؟

   4.5 التوافق والخطية

   4.6 مصطلحان للخسارة

4. مناقشة

   5.1 العمل المستقبلي

   5.2 الخاتمة، شكر وتقدير، والمراجع

الملحق

أ الملحق

أ.1 مجموعات البيانات

في تجاربنا نستخدم مجموعات بيانات جدولية أصلها من OpenML وتم تجميعها في مجموعة من مجموعات البيانات المرجعية من فريق Inria-Soda على HuggingFace [11]. نقدم بعض التفاصيل حول كل مجموعة بيانات:

\ التسويق المصرفي هذه مجموعة بيانات تصنيف ثنائية بستة ميزات إدخال وهي متوازنة تقريبًا من حيث الفئات. نقوم بالتدريب على 7,933 عينة تدريب واختبار على 2,645 عينة متبقية.

\ إسكان كاليفورنيا هذه مجموعة بيانات تصنيف ثنائية بسبع ميزات إدخال وهي متوازنة تقريبًا من حيث الفئات. نقوم بالتدريب على 15,475 عينة تدريب واختبار على 5,159 عينة متبقية.

\ الكهرباء هذه مجموعة بيانات تصنيف ثنائية بسبع ميزات إدخال وهي متوازنة تقريبًا من حيث الفئات. نقوم بالتدريب على 28,855 عينة تدريب واختبار على 9,619 عينة متبقية.

أ.2 المعلمات الفائقة

العديد من معلماتنا الفائقة ثابتة عبر جميع تجاربنا. على سبيل المثال، يتم تدريب جميع شبكات MLP بحجم دفعة 64، ومعدل تعلم أولي 0.0005. أيضًا، جميع شبكات MLP التي ندرسها تتكون من 3 طبقات مخفية من 100 عصبون لكل منها. نستخدم دائمًا محسن AdamW [19]. يختلف عدد العصور من حالة إلى أخرى. لجميع مجموعات البيانات الثلاث، نقوم بالتدريب لمدة 30 عصرًا عندما 𝜆 ∈ {0.0, 0.25} و 50 عصرًا في الحالات الأخرى. عند تدريب النماذج الخطية، نستخدم 10 عصور ومعدل تعلم أولي 0.1.

أ.3 مقاييس الاختلاف

نحدد هنا كل من مقاييس الاتفاق الستة المستخدمة في عملنا.

\ تعتمد المقاييس الأربعة الأولى على أهم 𝑘 ميزة في كل تفسير. دع 𝑡𝑜𝑝_𝑓 𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘) تمثل أهم 𝑘 ميزة في تفسير 𝐸، ودع 𝑟𝑎𝑛𝑘 (𝐸, 𝑠) تكون رتبة أهمية الميزة 𝑠 ضمن التفسير 𝐸، ودع 𝑠𝑖𝑔𝑛(𝐸, 𝑠) تكون إشارة (موجبة، سالبة، أو صفر) لدرجة أهمية الميزة 𝑠 في التفسير 𝐸.

\

\ مقياسا الاتفاق التاليان يعتمدان على جميع الميزات داخل كل تفسير، وليس فقط على أهم 𝑘. دع 𝑅 تكون دالة تحسب ترتيب الميزات داخل تفسير حسب الأهمية.

\

\ (ملاحظة: يحدد Krishna وآخرون [15] في ورقتهم أن 𝐹 يجب أن تكون مجموعة من الميزات يحددها المستخدم النهائي، ولكن في تجاربنا نستخدم جميع الميزات مع هذا المقياس).

أ.4 نتائج تجربة الميزات غير المفيدة

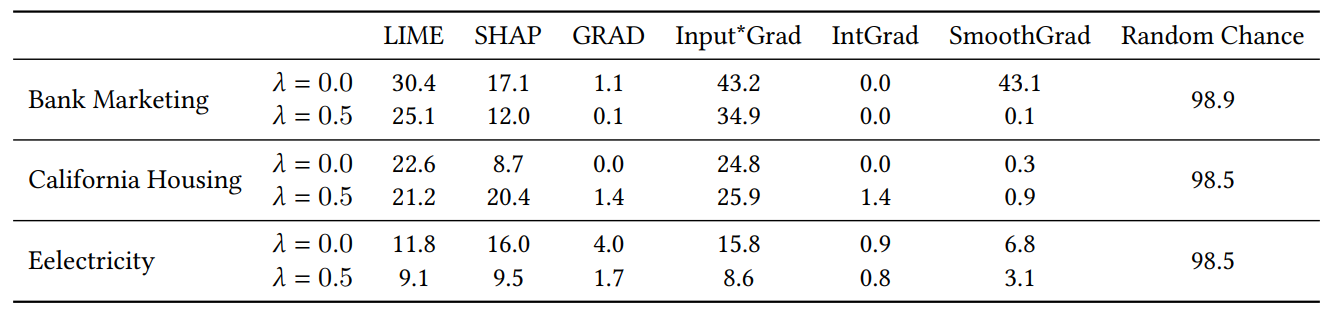
عندما نضيف ميزات عشوائية للتجربة في القسم 4.4، نضاعف عدد الميزات. نفعل ذلك للتحقق مما إذا كانت خسارة التوافق لدينا تضر بجودة التفسير من خلال وضع ميزات غير ذات صلة في أهم 𝐾 في كثير من الأحيان أكثر من النماذج المدربة بشكل طبيعي. في الجدول 1، نبلغ عن النسبة المئوية للوقت الذي تضمن فيه كل مفسر إحدى الميزات العشوائية في أهم 5 ميزات. نلاحظ أنه على مستوى الجميع، لا نرى زيادة منهجية في هذه النسب المئوية بين 𝜆 = 0.0 (نموذج MLP أساسي بدون خسارة التوافق لدينا) و 𝜆 = 0.5 (نموذج MLP مدرب مع خسارة التوافق لدينا)

\

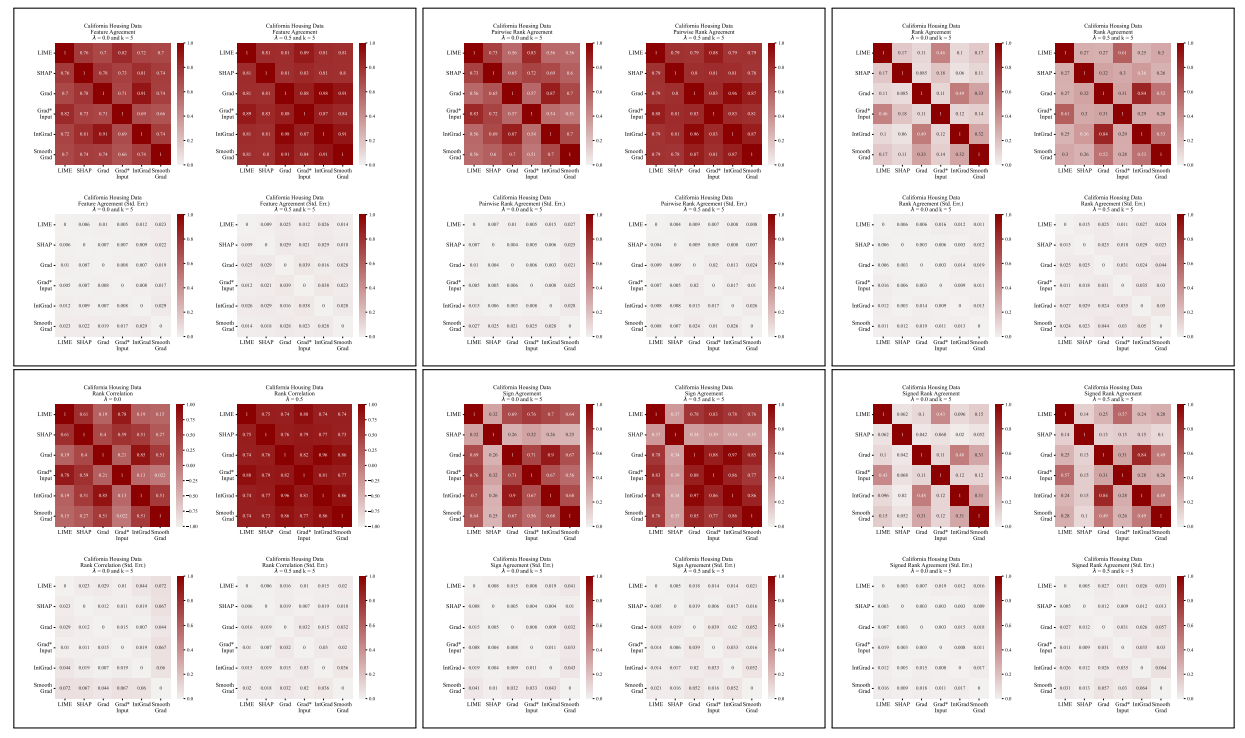
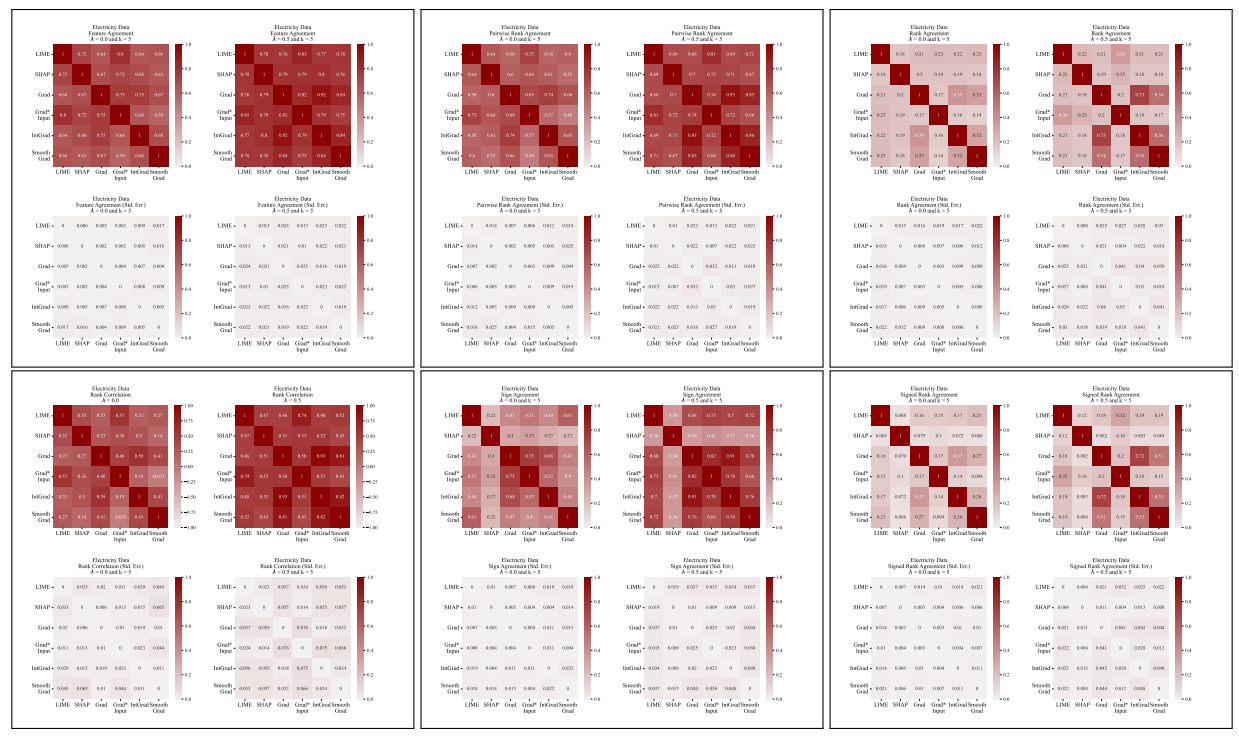
أ.5 المزيد من مصفوفات الاختلاف

\

\

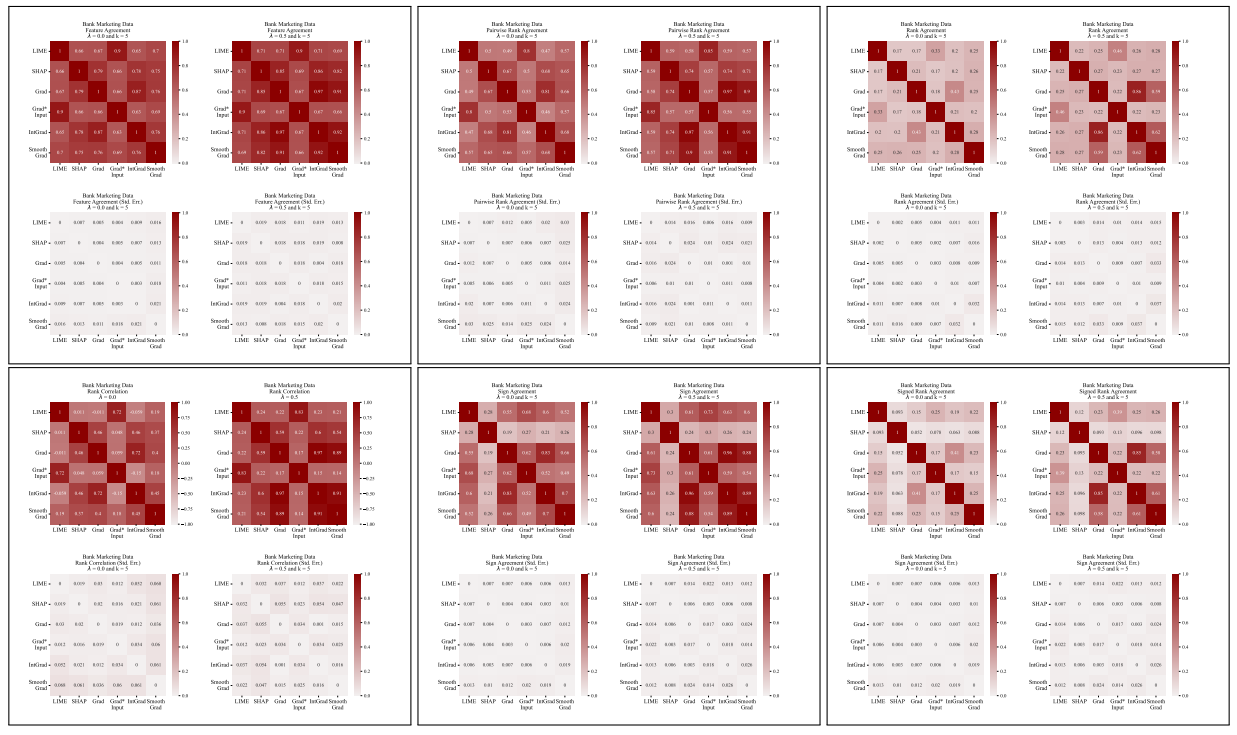
أ.6 النتائج الموسعة

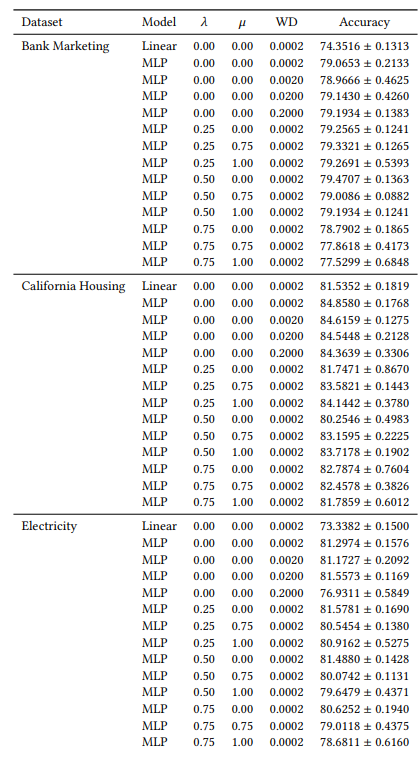
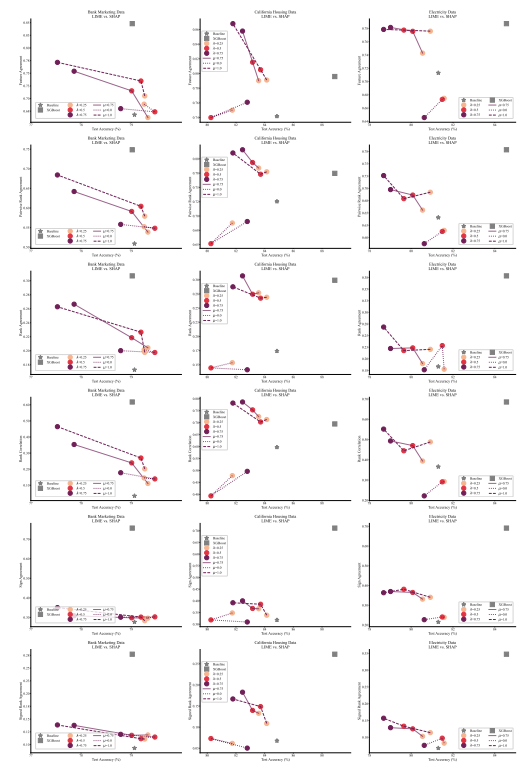
أ.7 رسومات إضافية

\

\

\

\

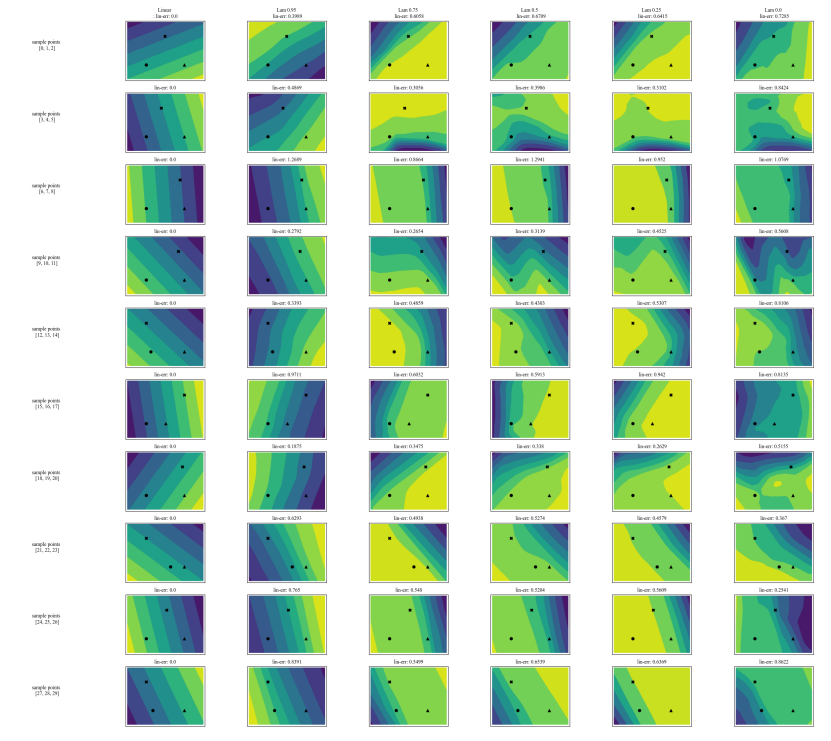
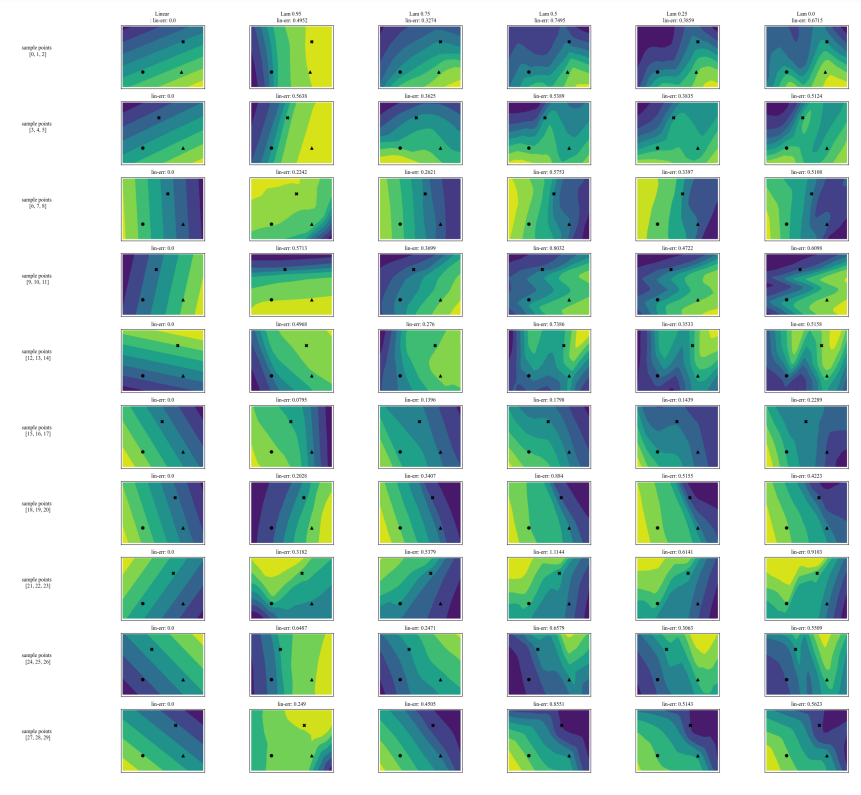
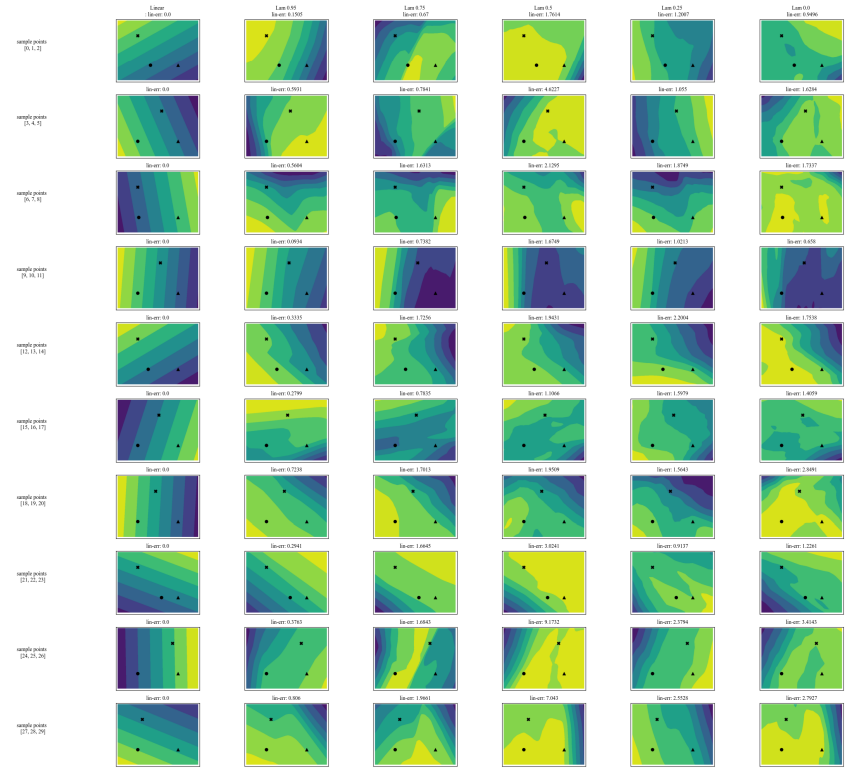
:::info المؤلفون:

(1) آفي شوارزشيلد، جامعة ماريلاند، كوليج بارك، ماريلاند، الولايات المتحدة الأمريكية والعمل المنجز أثناء العمل في آرثر (avi1umd.edu)؛

(2) ماكس سيمباليست، آرثر، مدينة نيويورك، نيويورك، الولايات المتحدة الأمريكية؛

(3) كارثيك راو، آرثر، مدينة نيويورك، نيويورك، الولايات المتحدة الأمريكية؛

(4) كيغان هاينز، آرثر، مدينة نيويورك، نيويورك، الولايات المتحدة الأمريكية؛

(5) جون ديكرسون†، آرثر، مدينة نيويورك، نيويورك، الولايات المتحدة الأمريكية (john@arthur.ai).

:::

:::info هذه الورقة متاحة على arxiv تحت ترخيص CC BY 4.0 DEED.

:::

\