كيف يسرع WormHole من إيجاد المسارات في الرسوم البيانية ذات المليارات من الحواف

جدول الروابط

نبذة مختصرة و 1. مقدمة

1.1 مساهمتنا

1.2 الإعداد

1.3 الخوارزمية

1. الأعمال ذات الصلة

2. الخوارزمية

   3.1 مرحلة التفكيك الهيكلي

   3.2 مرحلة التوجيه

   3.3 متغيرات WormHole

3. التحليل النظري

   4.1 المقدمات

   4.2 دون الخطية للحلقة الداخلية

   4.3 خطأ التقريب

   4.4 تعقيد الاستعلام

4. النتائج التجريبية

   5.1 WormHole𝐸 و WormHole𝐻 و BiBFS

   5.2 مقارنة مع طرق قائمة على المؤشر

   5.3 WormHole كأساس: WormHole𝑀

المراجع

1.1 مساهمتنا

قمنا بتصميم خوارزمية جديدة، WormHole، التي تنشئ بنية بيانات تسمح لنا بالإجابة على استفسارات متعددة حول أقصر المسارات من خلال استغلال الهيكل النموذجي للعديد من الشبكات الاجتماعية والمعلوماتية. WormHole بسيطة وسهلة التنفيذ ومدعومة نظريًا. نقدم عدة متغيرات منها، كل منها مناسب لإعداد مختلف، مما يظهر نتائج تجريبية ممتازة على مجموعة متنوعة من مجموعات بيانات الشبكة. فيما يلي بعض ميزاتها الرئيسية:

\ • المفاضلة بين الأداء والدقة. على حد علمنا، خوارزميتنا هي أول خوارزمية تقريبية دون خطية لأقصر المسارات في الشبكات الكبيرة. حقيقة أننا نسمح بخطأ إضافي صغير، يؤدي إلى مفاضلة بين وقت/مساحة المعالجة المسبقة ووقت الاستفسار، ويسمح لنا بالتوصل

\

\ إلى حل مع معالجة مسبقة فعالة ووقت استفسار سريع. من الجدير بالذكر أن أكثر متغيراتنا دقة (ولكن الأبطأ)، WormHole𝐸، لديه دقة شبه مثالية: أكثر من 90٪ من الاستفسارات تتم الإجابة عليها بدون خطأ إضافي، وفي جميع الشبكات، تتم الإجابة على أكثر من 99٪ من الاستفسارات بخطأ إضافي لا يتجاوز 2. انظر الجدول 3 لمزيد من التفاصيل.

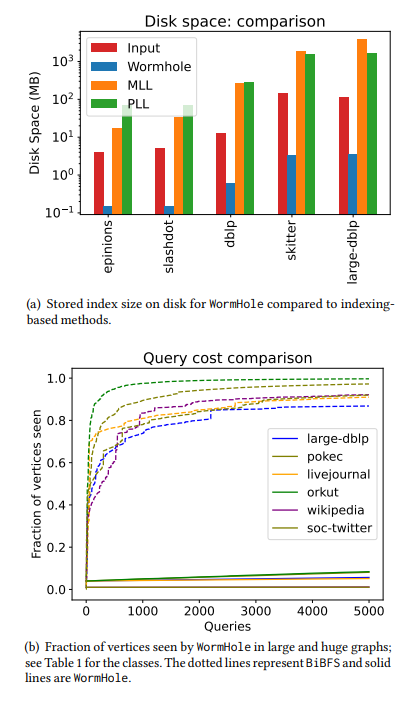
\ • وقت إعداد سريع للغاية. كان أطول وقت لإنشاء المؤشر لدينا دقيقتين فقط حتى للرسوم البيانية ذات المليار حافة. للسياق، استنفدت PLL و MLL الوقت على نصف الشبكات التي اختبرناها، وبالنسبة للرسوم البيانية متوسطة الحجم حيث أنهت PLL و MLL عملياتها، كان إنشاء مؤشر WormHole أسرع بـ 100 مرة. أي أن WormHole انتهى في ثوانٍ بينما استغرقت PLL ساعات. انظر الجدول 4 والجدول 5. يتحقق وقت الإعداد السريع هذا بسبب استخدام مؤشر ذو حجم دون خطي. بالنسبة لأكبر الشبكات التي نظرنا فيها، يكفي أخذ مؤشر حوالي 1٪ من العقد للحصول على خطأ إضافي متوسط صغير - انظر الجدول 1. بالنسبة للشبكات الأصغر، قد يصل إلى 6٪.

\ • وقت استفسار سريع. مقارنة بـ BiBFS، فإن الإصدار الأساسي WormHole𝐸 (بدون أي تحسينات قائمة على المؤشر) أسرع بمرتين لجميع الرسوم البيانية تقريبًا وأسرع بأكثر من 4 مرات على أكبر ثلاثة رسوم بيانية اختبرناها. يحقق المتغير البسيط WormHole𝐻 تحسنًا بمقدار رتبة على حساب الدقة: أسرع بشكل متسق بـ 20 مرة عبر جميع الرسوم البيانية تقريبًا، وأكثر من 180 مرة للرسم البياني الأكبر لدينا. انظر الجدول 3 للمقارنة الكاملة. عادة ما تجيب الطرق القائمة على الفهرسة على الاستفسارات في ميكروثانية؛ كلا المتغيرين المذكورين أعلاه لا يزالان في نظام الميلي ثانية.

\ • الجمع بين WormHole وأحدث التقنيات. تعمل WormHole عن طريق تخزين مجموعة فرعية صغيرة من الرؤوس التي نحسب عليها أقصر المسارات بدقة. للاستفسارات العشوائية، نوجه مسارنا من خلال هذه المجموعة الفرعية، التي نسميها النواة. نستخدم هذه الرؤية لتقديم متغير ثالث، WormHole𝑀 من خلال تنفيذ أحدث التقنيات لأقصر المسارات، MLL، على النواة. يحقق هذا أوقات استفسار مماثلة لـ MLL (مع نفس ضمان الدقة مثل WormHole𝐻) بجزء من تكلفة الإعداد، ويعمل للرسوم البيانية الضخمة حيث لا تنتهي MLL. نستكشف هذا النهج المشترك في §5.3، ونقدم إحصائيات في الجدول 6.

\ • تعقيد استعلام دون خطي. يشير تعقيد الاستعلام إلى عدد الرؤوس التي تستعلم عنها الخوارزمية. في نموذج الوصول المحدود للاستعلام حيث يكشف الاستعلام عن عقدة قائمة جيرانها (انظر §1.2)، يتناسب تعقيد الاستعلام لخوارزميتنا بشكل جيد جدًا مع عدد استفسارات المسافة / أقصر المسارات التي تم إجراؤها. للإجابة على 5000 استفسار تقريبي لأقصر المسارات، تلاحظ خوارزميتنا فقط بين 1٪ و 20٪ من العقد لمعظم الشبكات. بالمقارنة، ترى BiBFS أكثر من 90٪ من الرسم البياني للإجابة على بضع مئات من استفسارات أقصر المسارات. انظر الشكل 2 والشكل 5 للمقارنة.

\ • ضمانات قابلة للإثبات على الخطأ والأداء. في §4 نثبت مجموعة من النتائج النظرية التي تكمل وتشرح الأداء التجريبي. تم إثبات النتائج، المذكورة بشكل غير رسمي أدناه، لنموذج Chung-Lu للرسوم البيانية العشوائية مع توزيع درجة قانون القوة [15-17].

\ نظرية 1.1 (غير رسمية). في رسم بياني عشوائي Chung-Lu 𝐺 مع أس قانون القوة 𝛽 ∈ (2,3) على 𝑛 رأس، تتمتع WormHole بالضمانات التالية باحتمالية عالية:

\

\

:::info المؤلفون:

(1) تاليا إيدن، جامعة بار إيلان (talyaa01@gmail.com);

(2) عمري بن إليعازر، معهد ماساتشوستس للتكنولوجيا (omrib@mit.edu);

(3) سي. سيشادري، جامعة كاليفورنيا سانتا كروز (sesh@ucsc.edu).

:::

:::info هذه الورقة متاحة على arxiv تحت ترخيص CC BY 4.0.

:::

\