فهم خطأ التقريب وتعقيد الاستعلام في توجيه WormHole

جدول الروابط

نبذة مختصرة و 1. مقدمة

1.1 مساهمتنا

1.2 الإعداد

1.3 الخوارزمية

1. الأعمال ذات الصلة

2. الخوارزمية

   3.1 مرحلة التحليل الهيكلي

   3.2 مرحلة التوجيه

   3.3 متغيرات WormHole

3. التحليل النظري

   4.1 المقدمات

   4.2 دون الخطية للحلقة الداخلية

   4.3 خطأ التقريب

   4.4 تعقيد الاستعلام

4. النتائج التجريبية

   5.1 WormHole𝐸 و WormHole𝐻 و BiBFS

   5.2 مقارنة مع طرق قائمة على المؤشر

   5.3 WormHole كأساس: WormHole𝑀

المراجع

4.3 خطأ التقريب

الآن بعد أن أصبح لدينا حلقة داخلية دون خطية تحتوي على نواة Chung-Lu، يجب أن نظهر أن توجيه المسارات من خلالها يتسبب فقط في عقوبة صغيرة. بديهيًا، كلما كانت الحلقة الداخلية أكبر، كان من الأسهل تحقيق ذلك: إذا كانت الحلقة الداخلية هي الرسم البياني بأكمله، فإن البيان يصبح صحيحًا بشكل بديهي. لذلك يكمن التحدي في إظهار أننا يمكن أن نحقق ضمانًا قويًا من حيث الدقة حتى مع حلقة داخلية دون خطية. نثبت أن WormHole يتكبد خطأ إضافي بحد أقصى 𝑂(loglog𝑛) لجميع الأزواج، وهو أصغر بكثير من القطر Θ(log𝑛).

\

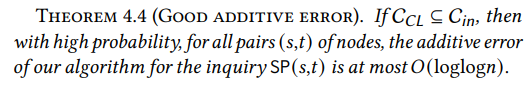
\ تصمد النتيجة المذكورة أعلاه باحتمالية عالية حتى في أسوأ الحالات. وتحديداً، لجميع أزواج (𝑠,𝑡) من الرؤوس في الرسم البياني، يكون طول المسار الذي يعيده WormHole أعلى بمقدار 𝑂(loglog𝑛) على الأكثر من المسافة الفعلية بين 𝑠 و 𝑡. وهذا يعني بشكل بديهي أن متوسط الخطأ الإضافي لـ WormHole، باحتمالية عالية، محدود بنفس المقدار.

\

\

4.4 تعقيد الاستعلام

تذكر نموذج استعلام العقدة في هذه الورقة (انظر §1.2): بدءًا من عقدة واحدة، يُسمح لنا بإجراء استعلامات بشكل متكرر، حيث يسترجع كل استعلام قائمة الجيران لعقدة 𝑣 من اختيارنا. نحن مهتمون بتعقيد الاستعلام، أي عدد الاستعلامات المطلوبة لإجراء عمليات معينة.

\ \

\ \ النتيجة الأولى هي الحد الأعلى لأدائنا.

\ \

\ \ مخطط الإثبات. بالنسبة لاستفسار معين SP(𝑢, 𝑣)، نعطي حدًا أعلى لتعقيد الاستعلام للـ BFS الذي يبدأ عند 𝑢، وبالمثل بالنسبة لـ 𝑣؛ إجمالي تعقيد الاستعلام هو مجموع هاتين الكميتين.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info المؤلفون:

(1) تاليا إيدن، جامعة بار-إيلان (talyaa01@gmail.com);

(2) عمري بن-إليعازر، معهد ماساتشوستس للتكنولوجيا (omrib@mit.edu);

(3) سي. سيشادري، جامعة كاليفورنيا سانتا كروز (sesh@ucsc.edu).

:::

:::info هذه الورقة متاحة على arxiv تحت ترخيص CC BY 4.0.

:::

\