সিন্থেটিক গাউসিয়ান এবং ট্রি এম্বেডিং-এ অপটিমাইজেশন পারফরম্যান্স
লিংকের সারণী
সারসংক্ষেপ এবং ১. ভূমিকা
-
সম্পর্কিত কাজ
-
হাইপারবলিক SVM-এর জন্য কনভেক্স রিলাক্সেশন কৌশল
৩.১ প্রাথমিক তথ্য
৩.২ HSVM-এর মূল সূত্রায়ন
৩.৩ সেমিডেফিনিট সূত্রায়ন
৩.৪ মোমেন্ট-সাম-অফ-স্কয়ার রিলাক্সেশন
-
পরীক্ষা-নিরীক্ষা
৪.১ সিন্থেটিক ডেটাসেট
৪.২ বাস্তব ডেটাসেট
-
আলোচনা, কৃতজ্ঞতা স্বীকার এবং তথ্যসূত্র
\
A. প্রমাণসমূহ
B. শিথিল সূত্রায়নে সমাধান নিষ্কাশন
C. মোমেন্ট সাম-অফ-স্কয়ার রিলাক্সেশন হায়ারার্কিতে
D. প্ল্যাট স্কেলিং [৩১]
E. বিস্তারিত পরীক্ষামূলক ফলাফল
F. দৃঢ় হাইপারবলিক সাপোর্ট ভেক্টর মেশিন
৪.১ সিন্থেটিক ডেটাসেট
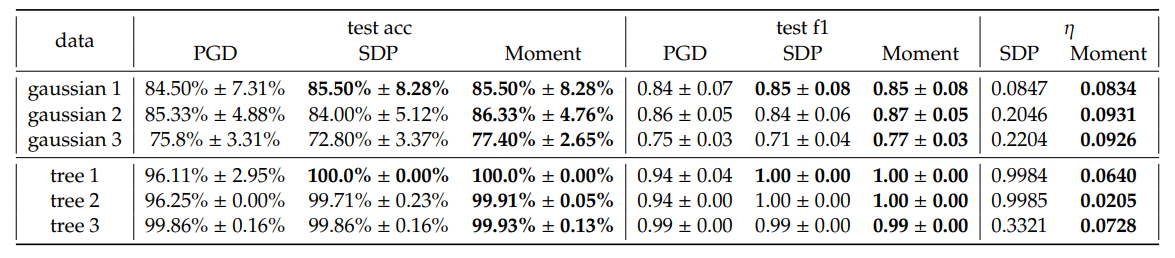
\ সাধারণত, আমরা PGD-এর তুলনায় SDP এবং Moment থেকে গড় পরীক্ষার নির্ভুলতা এবং ওজনযুক্ত F1 স্কোরে সামান্য লাভ পর্যবেক্ষণ করি। উল্লেখযোগ্যভাবে, আমরা দেখতে পাই যে Moment প্রায়শই SDP-এর তুলনায় বেশিরভাগ কনফিগারেশন জুড়ে আরও সামঞ্জস্যপূর্ণ উন্নতি দেখায়। এছাড়াও, Moment SDP-এর তুলনায় ছোট অপটিম্যালিটি গ্যাপ 𝜂 প্রদান করে। এটি আমাদের প্রত্যাশার সাথে মেলে যে Moment SDP-এর চেয়ে আরও দৃঢ়।
\ যদিও কিছু ক্ষেত্রে, উদাহরণস্বরূপ যখন 𝐾 = ৫, Moment PGD এবং SDP উভয়ের তুলনায় উল্লেখযোগ্যভাবে ছোট ক্ষতি অর্জন করে, এটি সাধারণত এমন নয়। আমরা জোর দিয়ে বলছি যে এই ক্ষতিগুলি ম্যাক্স-মার্জিন হাইপারবলিক সেপারেটরদের সাধারণীকরণযোগ্যতার সরাসরি পরিমাপ নয়; বরং, এগুলি মার্জিন সর্বাধিকীকরণ এবং ভুল শ্রেণীবিভাগের জন্য শাস্তির সংমিশ্রণ যা 𝐶-এর সাথে স্কেল করে। তাই, পরীক্ষার নির্ভুলতা এবং ওজনযুক্ত F1 স্কোরে কর্মক্ষমতা ভাল হওয়ার পর্যবেক্ষণ, যদিও SDP এবং Moment থেকে নিষ্কাশিত সমাধান ব্যবহার করে গণনা করা ক্ষতি কখনও কখনও PGD-এর তুলনায় বেশি, জটিল ক্ষতি ল্যান্ডস্কেপের কারণে হতে পারে। আরও নির্দিষ্টভাবে, ক্ষতিতে পর্যবেক্ষিত বৃদ্ধি অপটিমাইজেশন পদ্ধতির কার্যকারিতার পরিবর্তে ল্যান্ডস্কেপের জটিলতার জন্য দায়ী করা যেতে পারে। নির্ভুলতা এবং F1 স্কোর ফলাফলের উপর ভিত্তি করে, অভিজ্ঞতামূলকভাবে SDP এবং Moment পদ্ধতিগুলি এমন সমাধান চিহ্নিত করে যা শুধুমাত্র গ্রেডিয়েন্ট ডিসেন্ট চালিয়ে প্রাপ্ত সমাধানের চেয়ে ভাল সাধারণীকরণ করে। আমরা পরিশিষ্ট E.2-এ হাইপারপ্যারামিটারের প্রভাব এবং সারণী ৪-এ রানটাইম সম্পর্কে আরও বিস্তারিত বিশ্লেষণ প্রদান করি। গাউসিয়ান ১-এর জন্য সিদ্ধান্ত সীমানা চিত্র ৫-এ দৃশ্যমান করা হয়েছে।
\ ![চিত্র ৩: তিনটি সিন্থেটিক গাউসিয়ান (উপরের সারি) এবং তিনটি ট্রি এম্বেডিং (নিচের সারি)। সমস্ত বৈশিষ্ট্য H2-এ রয়েছে কিন্তু B2-এ স্টেরিওগ্রাফিক প্রজেকশনের মাধ্যমে দৃশ্যমান করা হয়েছে। বিভিন্ন রঙ বিভিন্ন শ্রেণী প্রতিনিধিত্ব করে। ট্রি ডেটাসেটের জন্য, গ্রাফ সংযোগগুলিও দৃশ্যমান করা হয়েছে কিন্তু প্রশিক্ষণে ব্যবহার করা হয়নি। নির্বাচিত ট্রি এম্বেডিংগুলি সরাসরি Mishne et al. [৬] থেকে এসেছে।](https://cdn.hackernoon.com/images/null-yv132j7.png)
\ সিন্থেটিক ট্রি এম্বেডিং। যেহেতু হাইপারবলিক স্পেসগুলি ট্রি এম্বেড করার জন্য ভাল, আমরা র্যান্ডম ট্রি গ্রাফ তৈরি করি এবং Mishne et al. [৬] অনুসরণ করে সেগুলি H2-এ এম্বেড করি। বিশেষভাবে, যদি নোডগুলি একটি নির্দিষ্ট নোডের সন্তান হয় তবে আমরা সেগুলিকে পজিটিভ হিসাবে লেবেল করি এবং অন্যথায় নেগেটিভ হিসাবে। আমাদের মডেলগুলি তারপর সাবট্রি শ্রেণীবিভাগের জন্য মূল্যায়ন করা হয়, যার লক্ষ্য একটি সীমানা চিহ্নিত করা যা একই সাবট্রির মধ্যে সমস্ত সন্তান নোড অন্তর্ভুক্ত করে। এই ধরনের কাজের বিভিন্ন ব্যবহারিক প্রয়োগ রয়েছে। উদাহরণস্বরূপ, যদি ট্রিটি টোকেনের একটি সেট প্রতিনিধিত্ব করে, তবে সিদ্ধান্ত সীমানা হাইপারবলিক স্পেসে শব্দার্থিক অঞ্চলগুলি হাইলাইট করতে পারে যা ডেটা গ্রাফের সাবট্রির সাথে সম্পর্কিত। আমরা জোর দিয়ে বলি যে এই ধরনের সাবট্রি শ্রেণীবিভাগ কাজে একটি সাধারণ বৈশিষ্ট্য হল ডেটা ভারসাম্যহীনতা, যা সাধারণত দুর্বল সাধারণীকরণযোগ্যতার দিকে নিয়ে যায়। তাই, আমরা এই চ্যালেঞ্জিং সেটিংয়ের অধীনে আমাদের পদ্ধতিগুলির কর্মক্ষমতা মূল্যায়ন করতে এই কাজটি ব্যবহার করার লক্ষ্য রাখি। তিনটি এম্বেডিং নির্বাচন করা হয়েছে এবং চিত্র ৩-এ দৃশ্যমান করা হয়েছে এবং কর্মক্ষমতা সারণী ১-এ সংক্ষিপ্ত করা হয়েছে। নির্বাচিত ট্রিগুলির রানটাইম সারণী ৪-এ পাওয়া যাবে। ট্রি ২-এর সিদ্ধান্ত সীমানা চিত্র ৬-এ দৃশ্যমান করা হয়েছে।
\ সিন্থেটিক গাউসিয়ান ডেটাসেটের ফলাফলের অনুরূপ, আমরা PGD-এর তুলনায় SDP এবং Moment থেকে ভাল কর্মক্ষমতা পর্যবেক্ষণ করি, এবং ডেটা ভারসাম্যহীনতার কারণে যা GD পদ্ধতিগুলি সাধারণত সংগ্রাম করে, এই ক্ষেত্রে আমরা ওজনযুক্ত F1 স্কোরে বড় লাভ পাই। এছাড়াও, আমরা SDP-এর জন্য বড় অপটিম্যালিটি গ্যাপ পর্যবেক্ষণ করি কিন্তু Moment-এর জন্য খুব টাইট গ্যাপ, যা শ্রেণী-ভারসাম্যহীনতা গুরুতর হলেও Moment-এর অপটিম্যালিটি প্রমাণ করে।
\ 
\
:::info লেখকগণ:
(১) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (shengyang@g.harvard.edu);
(২) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (peihanliu@fas.harvard.edu);
(৩) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, এবং Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA (cpehlevan@seas.harvard.edu)।
:::
:::info এই গবেষণাপত্রটি CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International) লাইসেন্সের অধীনে arxiv-এ উপলব্ধ।
:::
\
আপনি আরও পছন্দ করতে পারেন

PA দৈনিক প্রতিবেদন | Binance USD1 সরবরাহের ৮৭% ধারণ করে; বাজার মনোভাব নিম্ন, তবে He Yi বলেন FUD কমে গেলে আবার বৃদ্ধি পাবে।

মিস্টার বিস্ট ক্রিপ্টো কয়েন স্পটলাইটে, কিন্তু স্মার্ট বিনিয়োগকারীরা ১০০X সম্ভাবনা সহ DeepSnitch AI-তে দ্বিগুণ বিনিয়োগ করছেন, Bitwise CEO বলেছেন ডাউনট্রেন্ডের মধ্যে Bitcoin-এর জন্য প্রাতিষ্ঠানিক চাহিদা বেশি
