Der Geek-Leitfaden zum ML-Experimentieren

Tabelle der Links

Abstrakt und 1. Einleitung

1.1 Post-Hoc-Erklärung

1.2 Das Uneinigkeitsproblem

1.3 Förderung des Erklärungskonsenses

1. Verwandte Arbeiten

2. Pear: Post-HOC-Explainer-Agreement-Regularizer

3. Die Wirksamkeit des Konsens-Trainings

   4.1 Übereinstimmungsmetriken

   4.2 Verbesserung der Konsensmetriken

   [4.3 Konsistenz zu welchem Preis?]()

   4.4 Sind die Erklärungen noch wertvoll?

   4.5 Konsens und Linearität

   4.6 Zwei Verlustterme

4. Diskussion

   5.1 Zukünftige Arbeit

   5.2 Fazit, Danksagungen und Referenzen

Anhang

A ANHANG

A.1 Datensätze

In unseren Experimenten verwenden wir tabellarische Datensätze, die ursprünglich von OpenML stammen und vom Inria-Soda-Team auf HuggingFace [11] zu einem Satz von Benchmark-Datensätzen zusammengestellt wurden. Wir geben einige Details zu jedem Datensatz an:

\ Bank Marketing Dies ist ein binärer Klassifikationsdatensatz mit sechs Eingabemerkmalen und ist ungefähr klassenbalanciert. Wir trainieren mit 7.933 Trainingsproben und testen mit den verbleibenden 2.645 Proben.

\ California Housing Dies ist ein binärer Klassifikationsdatensatz mit sieben Eingabemerkmalen und ist ungefähr klassenbalanciert. Wir trainieren mit 15.475 Trainingsproben und testen mit den verbleibenden 5.159 Proben.

\ Electricity Dies ist ein binärer Klassifikationsdatensatz mit sieben Eingabemerkmalen und ist ungefähr klassenbalanciert. Wir trainieren mit 28.855 Trainingsproben und testen mit den verbleibenden 9.619 Proben.

A.2 Hyperparameter

Viele unserer Hyperparameter sind über alle unsere Experimente hinweg konstant. Zum Beispiel werden alle MLPs mit einer Batch-Größe von 64 und einer anfänglichen Lernrate von 0,0005 trainiert. Außerdem haben alle von uns untersuchten MLPs 3 versteckte Schichten mit jeweils 100 Neuronen. Wir verwenden immer den AdamW-Optimierer [19]. Die Anzahl der Epochen variiert von Fall zu Fall. Für alle drei Datensätze trainieren wir 30 Epochen, wenn 𝜆 ∈ {0,0, 0,25} und sonst 50 Epochen. Beim Training linearer Modelle verwenden wir 10 Epochen und eine anfängliche Lernrate von 0,1.

A.3 Uneinigkeitsmetriken

Wir definieren hier jede der sechs Übereinstimmungsmetriken, die in unserer Arbeit verwendet werden.

\ Die ersten vier Metriken hängen von den Top-𝑘 wichtigsten Merkmalen in jeder Erklärung ab. Lassen Sie 𝑡𝑜𝑝_𝑓 𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘) die Top-𝑘 wichtigsten Merkmale in einer Erklärung 𝐸 darstellen, lassen Sie 𝑟𝑎𝑛𝑘 (𝐸, 𝑠) den Wichtigkeitsrang des Merkmals 𝑠 innerhalb der Erklärung 𝐸 sein, und lassen Sie 𝑠𝑖𝑔𝑛(𝐸, 𝑠) das Vorzeichen (positiv, negativ oder null) des Wichtigkeitswerts des Merkmals 𝑠 in der Erklärung 𝐸 sein.

\

\ Die nächsten zwei Übereinstimmungsmetriken hängen von allen Merkmalen innerhalb jeder Erklärung ab, nicht nur von den Top-𝑘. Lassen Sie 𝑅 eine Funktion sein, die die Rangfolge der Merkmale innerhalb einer Erklärung nach Wichtigkeit berechnet.

\

\ (Hinweis: Krishna et al. [15] geben in ihrem Papier an, dass 𝐹 eine vom Endbenutzer angegebene Menge von Merkmalen sein soll, aber in unseren Experimenten verwenden wir alle Merkmale mit dieser Metrik).

A.4 Ergebnisse des Junk-Feature-Experiments

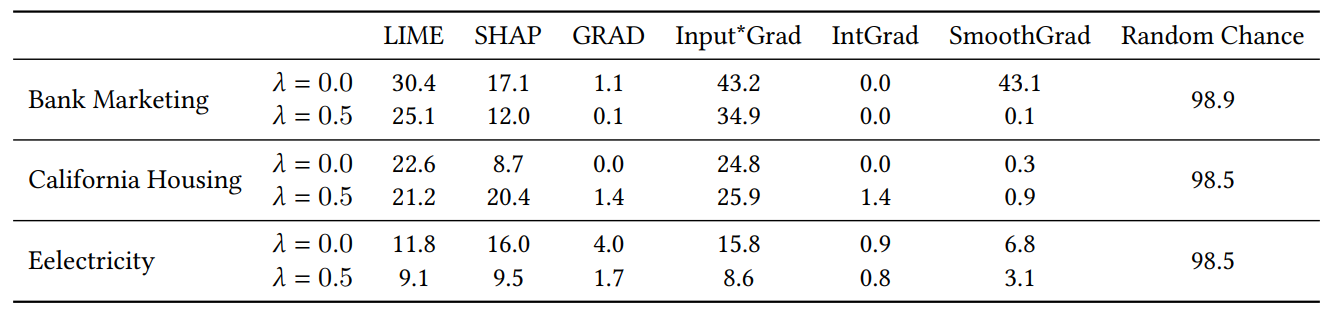
Wenn wir zufällige Merkmale für das Experiment in Abschnitt 4.4 hinzufügen, verdoppeln wir die Anzahl der Merkmale. Wir tun dies, um zu überprüfen, ob unser Konsensverlust die Erklärungsqualität beeinträchtigt, indem irrelevante Merkmale häufiger in die Top-𝐾 aufgenommen werden als bei natürlich trainierten Modellen. In Tabelle 1 berichten wir den prozentualen Anteil der Zeit, in der jeder Erklärer eines der zufälligen Merkmale in die 5 wichtigsten Merkmale aufgenommen hat. Wir beobachten, dass wir über alle Bereiche hinweg keinen systematischen Anstieg dieser Prozentsätze zwischen 𝜆 = 0,0 (ein Baseline-MLP ohne unseren Konsensverlust) und 𝜆 = 0,5 (ein MLP, das mit unserem Konsensverlust trainiert wurde) sehen

\

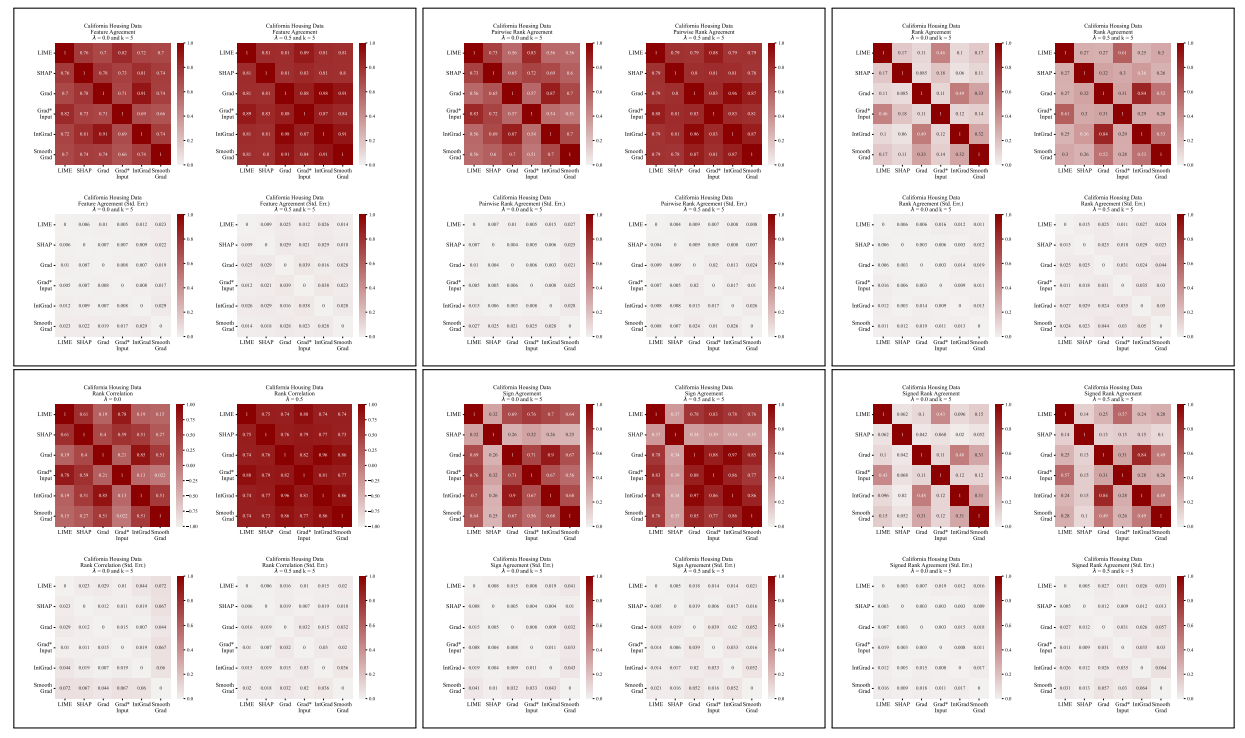
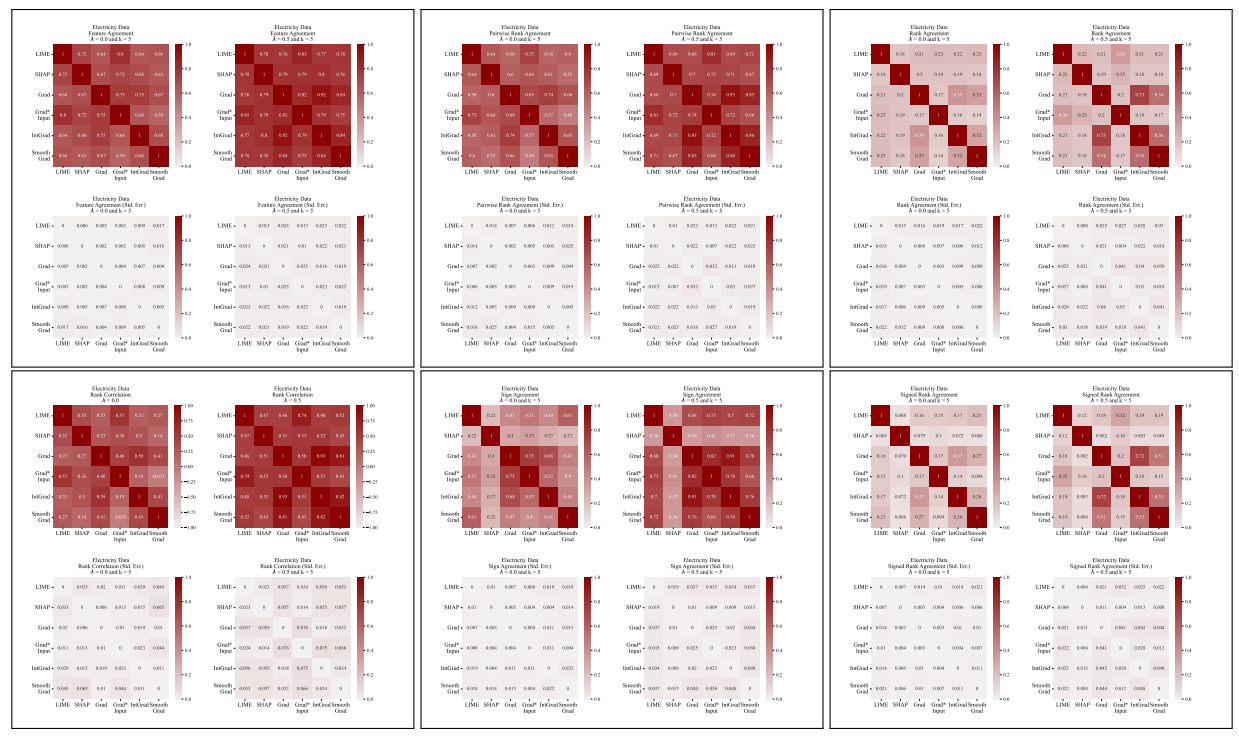
A.5 Weitere Uneinigkeitsmatrizen

\

\

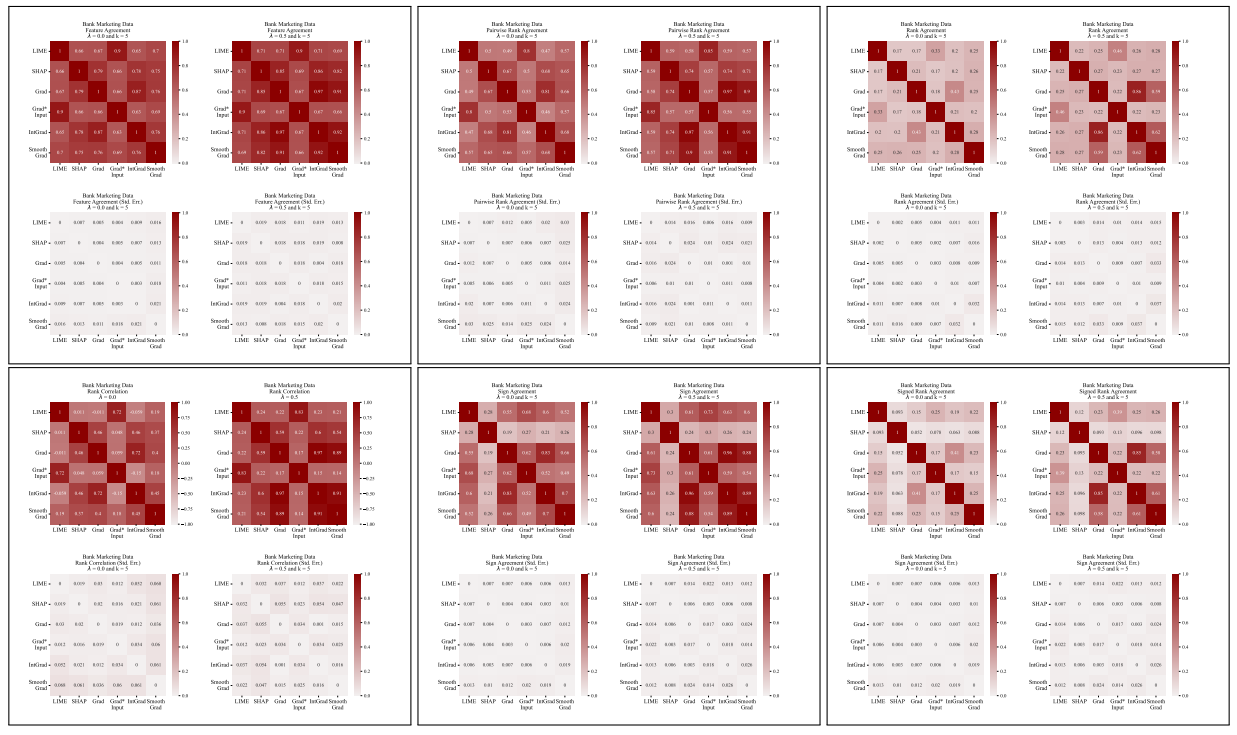
A.6 Erweiterte Ergebnisse

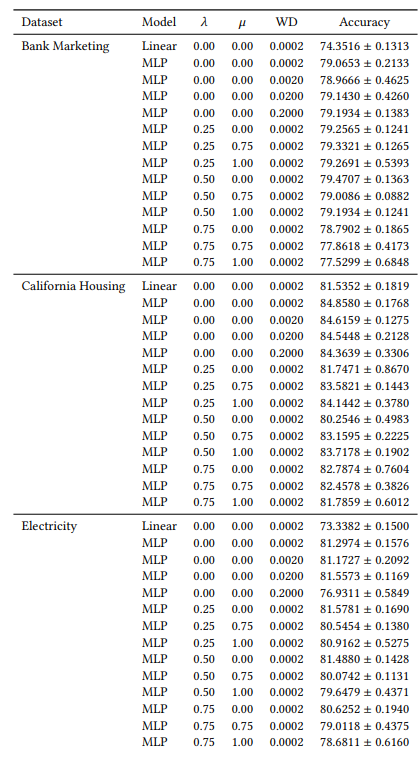
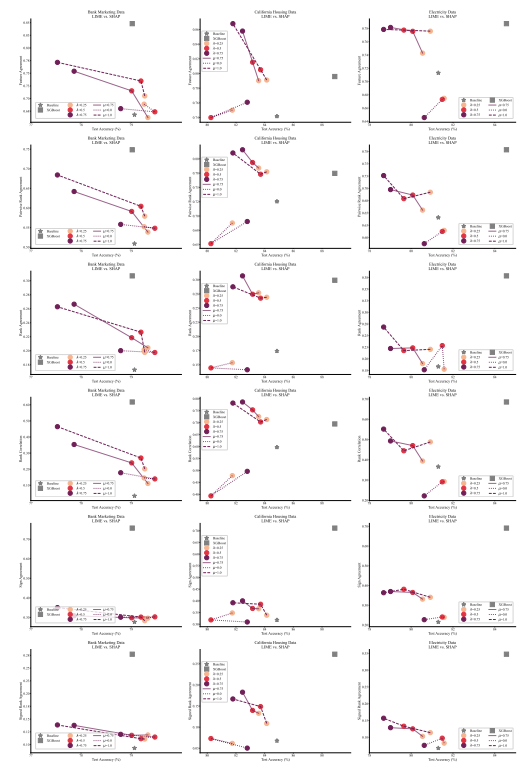
A.7 Zusätzliche Diagramme

\

\

\

\

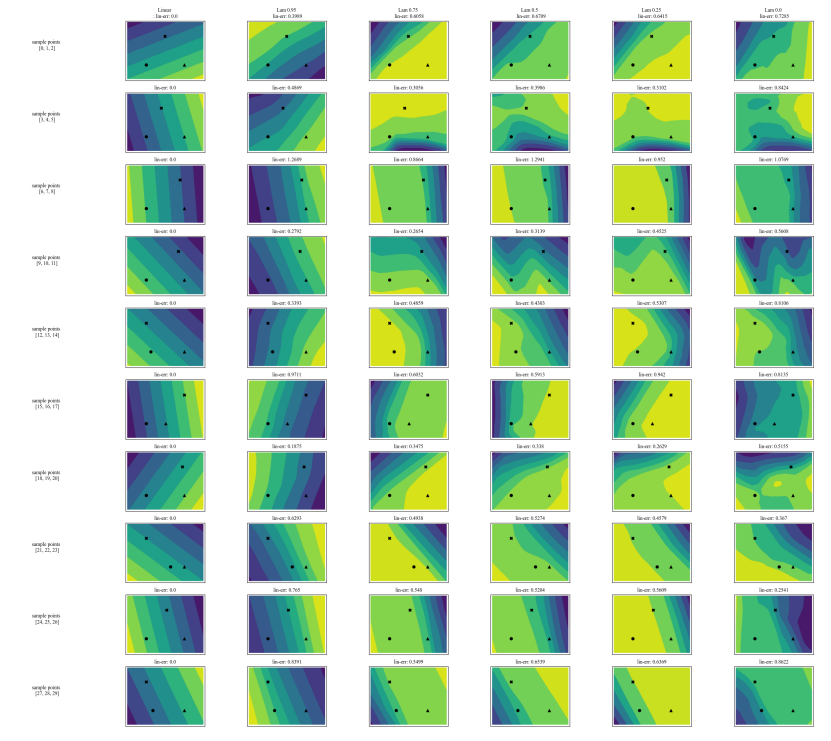
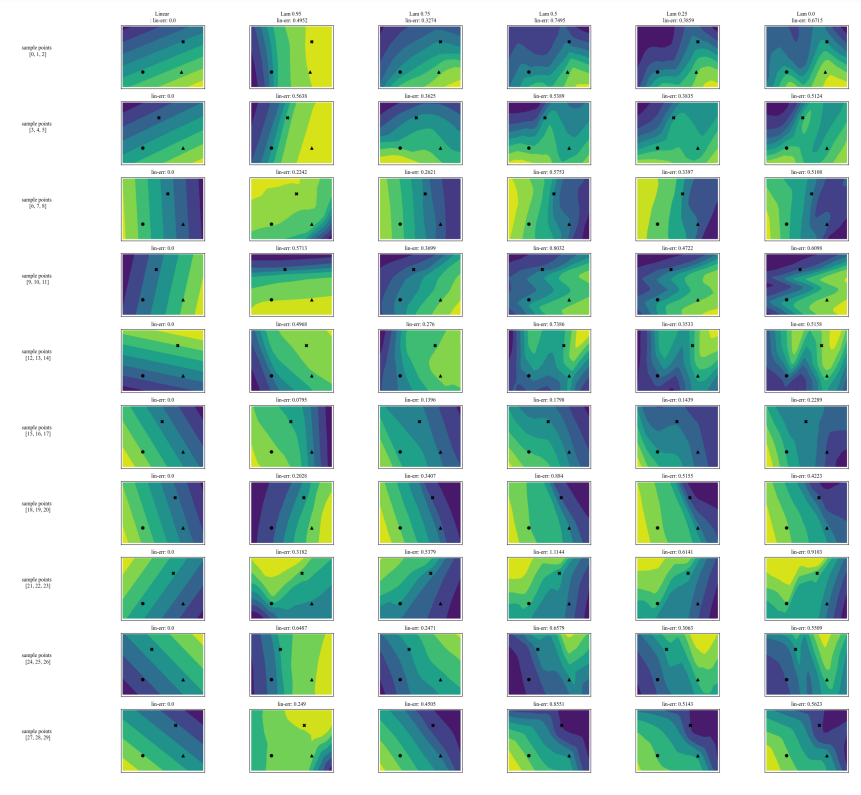
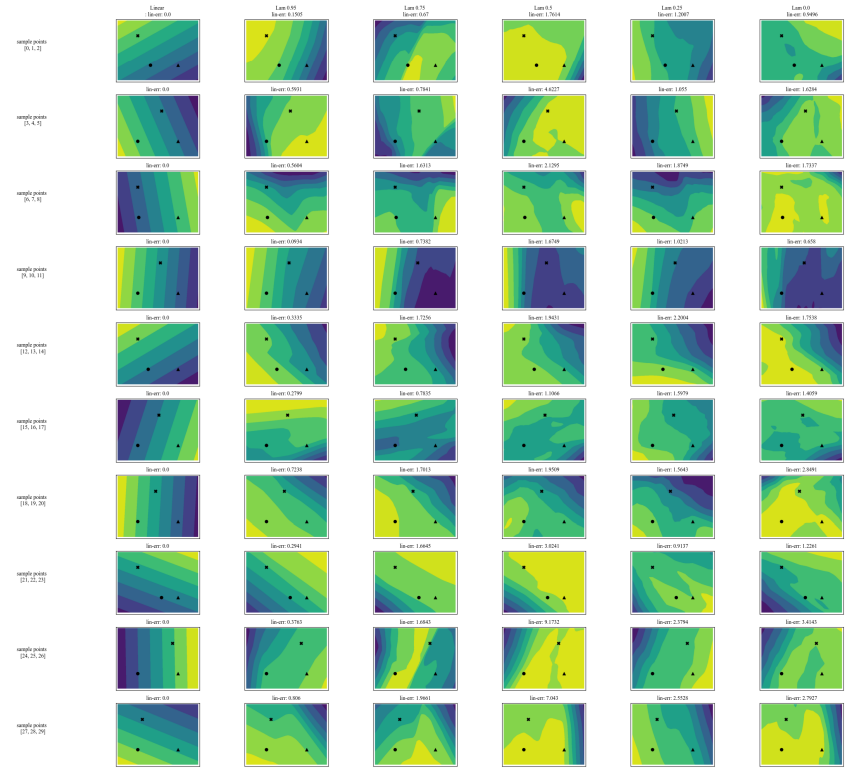
:::info Autoren:

(1) Avi Schwarzschild, University of Maryland, College Park, Maryland, USA und Arbeit abgeschlossen während der Tätigkeit bei Arthur (avi1umd.edu);

(2) Max Cembalest, Arthur, New York City, New York, USA;

(3) Karthik Rao, Arthur, New York City, New York, USA;

(4) Keegan Hines, Arthur, New York City, New York, USA;

(5) John Dickerson†, Arthur, New York City, New York, USA (john@arthur.ai).

:::

:::info Dieses Papier ist auf arxiv verfügbar unter der CC BY 4.0 DEED-Lizenz.

:::

\