BörseDEX+

Krypto kaufen Märkte Spot Futures500X Earn Events

Mehr

Goldbarren- & BTC-Giveaway2000g

Fraktale sind endlose Muster, die durch wiederholte mathematische Gleichungen entstehen. Wir werden eines der bekanntesten Fraktale zeichnen, nur mit Vanilla JS und der HTML5 Canvas API.Fraktale sind endlose Muster, die durch wiederholte mathematische Gleichungen entstehen. Wir werden eines der bekanntesten Fraktale zeichnen, nur mit Vanilla JS und der HTML5 Canvas API.

Programmierung eines fraktalen Baums mit JavaScript und HTML5

Von: Hackernoon

2025/10/11 03:00

TREE$0.1182-4.67%

LL$0.007927-1.25%

\ Fraktale, diese rätselhaften Figuren, die überall sind, aber vom ungeübten Auge nicht gesehen werden können. Heute werden wir eines der bekanntesten Fraktale zeichnen, nur mit Vanilla JS und der HTML5 Canvas API. Lass uns coden!

Was du lernen wirst

Was ist ein Fraktalbaum?
Den Fraktalbaum in Vanilla JS schreiben
Jenseits des Fraktalbaums

Was ist ein Fraktalbaum?

Um einen Fraktalbaum zu definieren, müssen wir natürlich zuerst die Definition eines Fraktals kennen.

Fraktale sind endlose Muster, die durch wiederholte mathematische Gleichungen entstehen und die in jeder Größenordnung, auf jeder Zoomstufe, ungefähr gleich aussehen. Mit anderen Worten, ein geometrisches Objekt, dessen Grundstruktur, rau oder fragmentiert, sich in verschiedenen Maßstäben wiederholt.

Wenn wir also ein Fraktal teilen, sehen wir eine verkleinerte Kopie des Ganzen.

Benoit Mandelbrot, der den Begriff Fraktal 1975 prägte, sagte:

\ Ziemlich klar, oder?

Hier sind einige Beispiele:

Animated Von Koch Curve

\ Animated Sierpinski Carpet

Was ist nun ein Fraktalbaum?

Stell dir einen Ast vor, aus dem Äste hervorkommen, und dann zwei Äste aus jedem Ast, und so weiter... so sieht ein Fraktalbaum aus.

Seine Form stammt vom Sierpinski-Dreieck (oder Sierpinski-Dichtung).

Wie du sehen kannst, wird das eine zum anderen, wenn sich der Winkel zwischen den Ästen ändert:

From Sierpinski Triangle to Fractal

Heute werden wir mit einer Figur enden, die der Endform dieses GIFs ähnelt.

Den Fraktalbaum in Vanilla JS schreiben

Zunächst einmal, hier ist das Endprodukt (du kannst es unterwegs anpassen):

Final Fractal Tree

Lass uns das nun Schritt für Schritt zeichnen.

Zunächst initialisieren wir unsere index.html-Datei mit einem Canvas mit vernünftigen Abmessungen und einem Script-Tag, in dem unser gesamter JS-Code stehen wird.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script></script>   </body> </html>

Dann beginnen wir mit dem Schreiben unseres JavaScripts.

Wir initialisieren unser Canvas-Element in JS, indem wir über die Variable myCanvas darauf zugreifen und den 2D-Rendering-Kontext mit der Variable ctx (Kontext) erstellen.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");     </script>   </body> </html>

Die getContext-Methode fügt also Eigenschaften und Methoden hinzu, die es dir ermöglichen, in diesem Fall in 2D zu zeichnen.

Jetzt ist es Zeit zum Nachdenken. Wie können wir den Algorithmus zum Zeichnen eines Fraktalbaums definieren? Hmm... 🤔

Wir wissen, dass die Äste immer kleiner werden. Und dass jeder Ast mit zwei Ästen endet, die aus ihm herauskommen, einer nach links und einer nach rechts.

Mit anderen Worten, wenn ein Ast lang genug ist, füge zwei kleinere Äste daran an. Wiederhole.

Es klingt, als sollten wir irgendwo eine rekursive Anweisung verwenden, oder?

Zurück zum Code, wir definieren jetzt unsere Funktion fractalTree, die mindestens vier Argumente benötigt: die X- und Y-Koordinaten, wo der Ast beginnt, die Länge des Astes und seinen Winkel.

In unserer Funktion beginnen wir das Zeichnen mit der beginPath()-Methode und speichern dann den Zustand des Canvas mit der save()-Methode.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();       }     </script>   </body> </html>

Die beginPath-Methode wird oft verwendet, wenn du eine neue Linie oder Figur mit einem festen Stil beginnst, wie der gleichen Farbe entlang der gesamten Linie oder der gleichen Breite. Die save-Methode speichert einfach den gesamten Zustand des Canvas, indem sie den aktuellen Zustand auf einen Stapel legt.

Jetzt werden wir unseren Fraktalbaum zeichnen, indem wir eine Linie (Ast) zeichnen, den Canvas drehen, den nächsten Ast zeichnen und so weiter. Es geht so (ich erkläre jede Methode unter dem Code-Beispiel):

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, -15);           draw(0, -len, len*0.8, +15);            ctx.restore();       }       draw(400, 600, 120, 0)     </script>   </body> </html>

Wir fügen also zuerst drei Methoden hinzu: translate, rotate und moveTo, die den Canvas, seinen Ursprung und unseren "Stift" "bewegen", damit wir den Ast in unserem gewünschten Winkel zeichnen können. Es ist, als würden wir einen Ast zeichnen, dann diesen Ast zentrieren (indem wir den gesamten Canvas bewegen) und dann einen neuen Ast vom Ende unseres vorherigen Astes aus zeichnen.

Die letzten beiden Methoden vor der if-Anweisung sind lineTo und stroke; die erste fügt eine gerade Linie zum aktuellen Pfad hinzu, und die zweite rendert sie. Du kannst es dir so vorstellen: lineTo gibt den Befehl, und stroke führt ihn aus.

Jetzt haben wir eine if-Anweisung, die angibt, wann die Rekursion gestoppt werden soll, wann das Zeichnen gestoppt werden soll. Die restore-Methode, wie in den MDN-Dokumenten angegeben, "stellt den zuletzt gespeicherten Canvas-Zustand wieder her, indem der oberste Eintrag im Zeichnungszustandsstapel entfernt wird".

Nach der if-Anweisung haben wir den rekursiven Aufruf und einen weiteren Aufruf der restore-Methode. Und dann einen Aufruf der Funktion, die wir gerade beendet haben.

Führe den Code jetzt in deinem Browser aus. Du wirst endlich einen Fraktalbaum sehen!

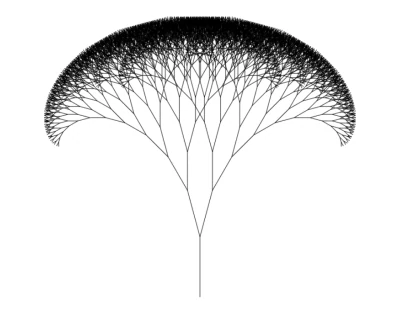
Fractal Tree First Iteration

Toll, oder? Jetzt machen wir es noch besser.

Wir fügen unserer draw-Funktion einen neuen Parameter hinzu, branchWidth, um unseren Fraktalbaum realistischer zu gestalten.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Bei jeder Iteration machen wir also jeden Ast dünner. Ich habe auch den Winkelparameter im rekursiven Aufruf geändert, um einen "offeneren" Baum zu erhalten.

Jetzt fügen wir etwas Farbe hinzu! Und Schatten, warum nicht.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.strokeStyle = "green";           ctx.fillStyle = "green";            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            ctx.shadowBlur = 15;           ctx.shadowColor = "rgba(0,0,0,0.8)";            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Beide Farbmethoden sind selbsterklärend (strokeStyle und fillStyle). Auch die Schattenmethoden, shadowBlur und shadowColor.

Und das war's! Speichere die Datei und öffne sie mit deinem Browser, um das Endprodukt zu sehen.

Jetzt ermutige ich dich, mit dem Code zu spielen! Ändere die shadowColor, den fillStyle, mache einen kürzeren oder längeren Fraktalbaum, ändere den Winkel oder versuche, Blätter hinzuzufügen, das sollte herausfordernd sein 😉

Jenseits des Fraktalbaums

Wie ich dir am Anfang dieses Beitrags gezeigt habe, gibt es verschiedene Fraktale. Es wird nicht einfach sein, all diese mit der Canvas API zu erstellen, aber es sollte möglich sein. Ich habe einige davon in der Programmiersprache C erstellt

Haftungsausschluss: Die auf dieser Website veröffentlichten Artikel stammen von öffentlichen Plattformen und dienen ausschließlich zu Informationszwecken. Sie spiegeln nicht unbedingt die Ansichten von MEXC wider. Alle Rechte verbleiben bei den ursprünglichen Autoren. Sollten Sie der Meinung sein, dass Inhalte die Rechte Dritter verletzen, wenden Sie sich bitte an service@support.mexc.com um die Inhalte entfernen zu lassen. MEXC übernimmt keine Garantie für die Richtigkeit, Vollständigkeit oder Aktualität der Inhalte und ist nicht verantwortlich für Maßnahmen, die aufgrund der bereitgestellten Informationen ergriffen werden. Die Inhalte stellen keine finanzielle, rechtliche oder sonstige professionelle Beratung dar und sind auch nicht als Empfehlung oder Billigung von MEXC zu verstehen.