Einblick in die Logik von "Produkten" und Gleichheit in der Mengenlehre
Inhaltsverzeichnis
Abstrakt
- Danksagungen & Einleitung
2. Universelle Eigenschaften
3. Produkte in der Praxis
4. Universelle Eigenschaften in der algebraischen Geometrie
5. Das Problem mit Grothendiecks Verwendung der Gleichheit
6. Mehr über "kanonische" Abbildungen
7. Kanonische Isomorphismen in fortgeschrittener Mathematik
8. Zusammenfassung und Referenzen
Universelle Eigenschaften
Ich kenne drei vernünftige Klassen von Grundlagen für die Mathematik: solche, die auf Mengenlehre basieren, solche, die auf Typentheorie basieren, und solche, die auf Kategorientheorie basieren. Es gibt auch verschiedene Ergebnisse, die besagen, dass diese Grundlagen im Großen und Ganzen dieselben Theoreme beweisen können. Für eine Diskussion über Gleichheit müssen wir jedoch genau festlegen, worüber wir sprechen, und daher werde ich die ZFC-Mengenlehre und klassische Logik als Grundlage für unsere Diskussion wählen.1
Die Grundlage für diese Entscheidung ist einfach, dass wenn ein Mathematiker jemals einen Kurs über die logischen Grundlagen seines Fachs besucht hat (und viele haben das nicht), dann war es wahrscheinlich ein Kurs über Mengenlehre. Darüber hinaus ist die Literatur der reinen Mathematik in einem oberflächlich mengentheoretischen Stil geschrieben: Uns wird gesagt, dass eine Gruppe eine Menge mit einer bestimmten Struktur und Axiomen ist, eine Mannigfaltigkeit eine Menge mit einer anderen Struktur und Axiomen ist, und so weiter. Hier ist das Wort "Menge" nur ein Platzhalter für die Idee einer "Sammlung von Atomen".
Es ist offensichtlich, dass zwei Mengen, die gleich sind, dieselben Elemente haben; dies folgt aus dem sogenannten Substitutionsprinzip für Gleichheit, das besagt, dass wenn X und Y zwei beliebige mathematische Objekte sind, die gleich sind, dann ist jede Behauptung, die man in seinem Grundlagensystem über X machen kann, auch für Y wahr. Die Umkehrung, dass zwei Mengen mit denselben Elementen gleich sind, wird als Axiom der Theorie auferlegt. Dies stellt sicher, dass das abstrakte Konzept einer Menge mit unserem mentalen Modell dessen, was es repräsentiert, übereinstimmt: Eine Menge ist nicht mehr und nicht weniger als eine Sammlung von Dingen.
Nun möchte ich mit der Diskussion von Eigenschaften beginnen, die ein mathematisches Objekt eindeutig charakterisieren. Beginnen wir mit einem Beispiel: dem Produkt X × Y zweier Mengen X und Y. Ich möchte den Leser jetzt warnen, dass ich in den nächsten Absätzen einen sehr sorgfältigen Unterschied zwischen dem Konzept des Produkts von X und Y und dem Konzept eines Produkts von X und Y machen werde. Das Produkt X × Y zweier Mengen ist definiert als die Menge der geordneten Paare (x, y) mit x ∈ X und y ∈ Y (man kann anhand der Axiome der Mengenlehre überprüfen, dass es möglich ist, diese Menge zu erstellen).
Beachten Sie, dass wir hier auf dasselbe Problem stoßen, das wir bereits bei den reellen Zahlen gesehen haben: Es gibt mehrere verschiedene Möglichkeiten, das Konzept eines geordneten Paares in der Mengenlehre zu definieren. Die Mengenlehre ist sehr gut darauf ausgelegt, mit ungeordneten Paaren zu arbeiten: Die Mengen {x, y} und {y, x} haben dieselben Elemente und sind daher gleich, um ein geordnetes Paar zu definieren, muss man also eine Art Hack verwenden.
Die Wikipedia-Seite für geordnete Paare [Wik04b] gibt derzeit drei verschiedene Konstruktionen an, die auf Wiener ({{{x}, ∅}, {{y}}}), Hausdorff ({{x, 1}, {y, 2}}) und Kurotowski ({{x}, {x, y}}) zurückgehen; alle wirken etwas künstlich.2 Mathematiker sind sich durchaus bewusst, dass dieses Problem in der Praxis überhaupt keine Rolle spielt: Alles, was wir wissen müssen, ist die definierende Eigenschaft geordneter Paare, nämlich dass (x1, y1) = (x2, y2) ⇐⇒ x1 = x2 und y1 = y2; das ist alles, was wir brauchen werden, und alle Definitionen erfüllen diese Eigenschaft.
Das Produkt X × Y ist mit zwei Projektionsabbildungen π1 : X × Y → X und π2 : X × Y → Y ausgestattet. Streng genommen ist es nicht nur das Produkt, sondern das Tripel (X × Y, π1, π2), das die folgende universelle Eigenschaft erfüllt:
Die universelle Eigenschaft von Produkten: Ein Tripel (P, π1 : P → X, π2 : P → Y) wird ein Produkt von X und Y genannt, wenn es die folgende Eigenschaft erfüllt: Wenn S eine beliebige Menge ist und f : S → X und g : S → Y Funktionen sind, dann gibt es eine eindeutige Funktion von S nach P, so dass ihre Komposition mit π1 gleich f und ihre Komposition mit π2 gleich g ist.
Die universelle Eigenschaft ist keine Definition des Produkts zweier Mengen; sie kann als unendlich viele Fakten betrachtet werden, die ein Produkt erfüllen muss (eine für jede Wahl der Menge S und der Funktionen f und g). Es ist nicht schwer zu überprüfen, dass das Produkt X × Y von X und Y, ausgestattet mit den natürlichen Projektionen, ein Produkt ist. Aber die Umkehrung ist keineswegs wahr: Es gibt typischerweise viele andere Tripel (P, π1, π2), die die Eigenschaft erfüllen, ein Produkt zu sein, ohne das Produkt zu sein.
Wenn zum Beispiel X = {37} und Y = {42}, dann ist das Produkt X × Y gleich {(37, 42)}, aber tatsächlich erfüllt jede Menge P mit einem Element, ausgestattet mit π1 : P → X, die alles auf 37 abbildet, und π2 : P → Y, die alles auf 42 abbildet, die universelle Eigenschaft, ein Produkt zu sein. Insbesondere gibt es im Allgemeinen überabzählbar viele verschiedene Dinge, die die Eigenschaft erfüllen, ein Produkt zu sein. Mathematiker sind jedoch äußerst gut darin, diese verschiedenen Dinge zu identifizieren; sie sind "dasselbe" in einer Weise, die über die korrekte Verwendung des Symbols = hinausgeht. Wir können das aufgrund des Eindeutigkeits-Yoga für universelle Objekte tun. Gehen wir dieses Yoga, das ein Stück formaler kategorientheoretischer Unsinn ist, im Fall von Produkten durch.
Angenommen, P1 und P2 sind beide ein Produkt für X und Y. Die Anwendung des Existenzteils der universellen Eigenschaft für P2 (mit seinen Projektionen auf X und Y) auf die Menge S = P1 (mit ihren Projektionen auf X und Y) gibt uns eine Funktion α : P1 → P2, die mit den Projektionen auf X und Y kommutiert. Wenn wir die 1en und 2en im Argument vertauschen, können wir auch eine Funktion β : P2 → P1 konstruieren, die mit den Projektionen kommutiert. Darüber hinaus ist β ◦ α eine Abbildung von P1 nach P1, die mit den Projektionen kommutiert, ebenso wie die Identitätsfunktion; durch den Eindeutigkeitsteil der universellen Eigenschaft von P1, angewendet auf P1, schließen wir, dass β ◦ α die Identitätsabbildung auf P1 sein muss; ebenso muss α ◦ β die Identitätsabbildung auf P2 sein.
Daher sind α und β Bijektionen, die mit den Projektionsabbildungen kommutieren. Schließlich sagt uns der Eindeutigkeitsteil der universellen Eigenschaft für P2, angewendet auf P1, dass α die eindeutige Abbildung von P1 nach P2 ist, die mit den Projektionen kommutiert; symmetrisch ist β die eindeutige Abbildung von P2 nach P1, die mit den Projektionen kommutiert. Das Ergebnis dieses abstrakten Unsinns (der nie Elemente irgendeiner Menge erwähnte, nur Objekte und Morphismen) ist, dass es eindeutige gegenseitig inverse Bijektionen zwischen P1 und P2 gibt, die mit den Projektionen auf die Faktoren X und
Y kommutieren. Insbesondere, wenn P ein Produkt von X und Y ist, dann ist es eindeutig isomorph zum Produkt X × Y von X und Y in einer Weise, die mit den Projektionen kompatibel ist. In unserem Einelementbeispiel X = {37} und Y = {42}, wenn P eine beliebige Menge mit einem Element ist, dann sendet die eindeutige Abbildung von P nach X × Y das Element natürlich auf (37, 42).
:::info Autor: KEVIN BUZZARD
:::
:::info Dieser Artikel ist auf arxiv verfügbar unter der CC BY 4.0 DEED-Lizenz.
:::
\
Das könnte Ihnen auch gefallen
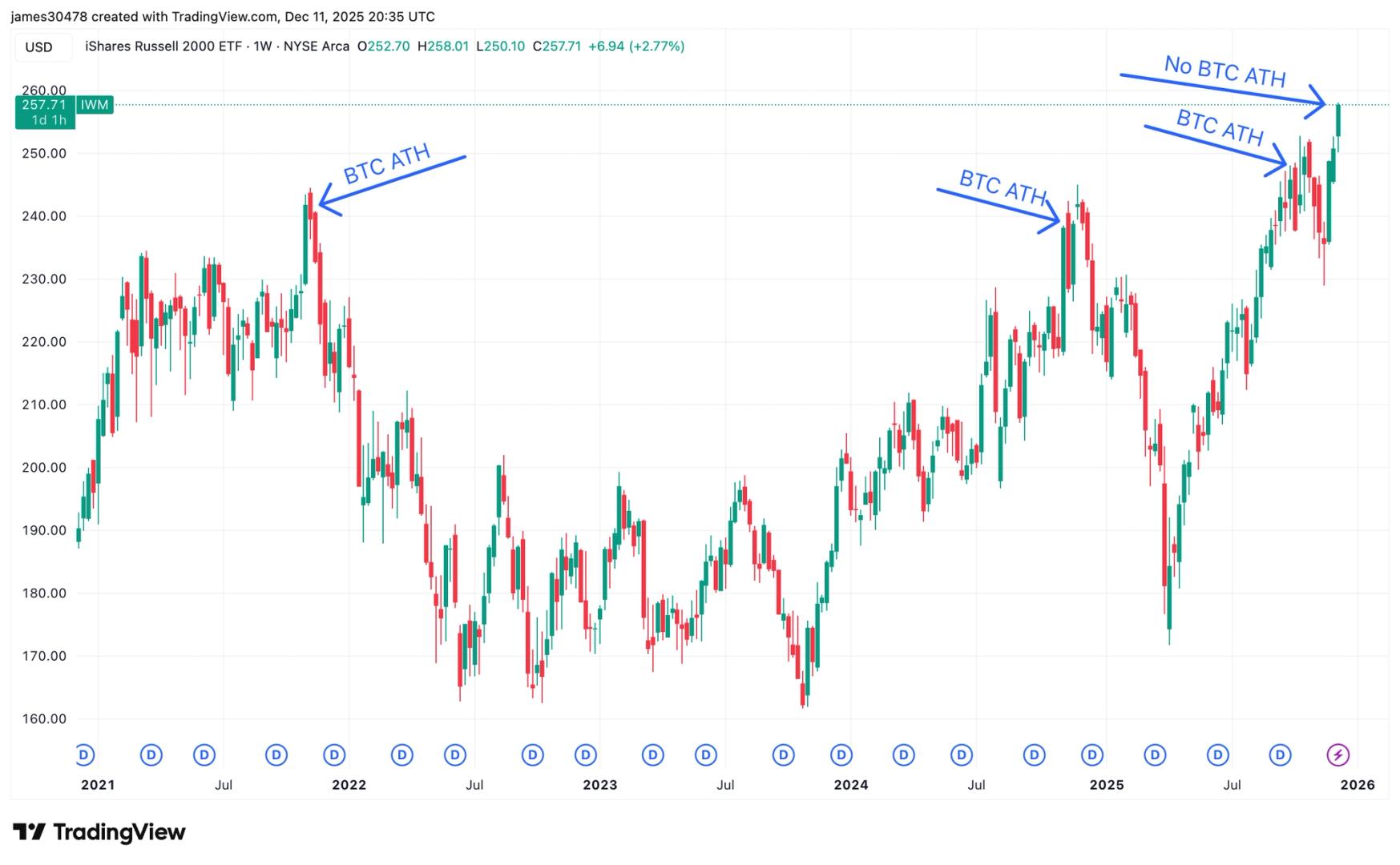
Von Gleichschritt zu Rückstand: Bitcoin bereit, zu Small-Cap-Höchstständen aufzuschließen
Link kopierenX (Twitter)LinkedInFacebookEmail

Fintechs führen Afrikas Bewertungstabelle für 2025 an, selbst während sich der Markt neu ausrichtet
