How HPPK DS Balances Security and Efficiency Across NIST Levels

Table of Links

Abstract and 1. Introduction

1. Contribution

2. Related Work

3. Brief of Homomorphic Polynomial Public Key Cryptography and 4.1 DPPK

   4.2 MPPK Key Encapsulation Mechanism

   4.3 HPPK KEM

   4.4 MPPK DS

4. HPPK Digital Signature Scheme

   5.1 HPPK DS Algorithm

   5.2 Signing

   5.3 Verify

   5.4 A Variant of the Barrett Reduction Algorithm

   5.5 A Toy Example

5. HPPK DS Security Analysis

6. Conclusion, References, Acknowledgements, and Author contributions statement

6 HPPK DS Security Analysis

\ In this section, we primarily outline the attacks we have identified on the HPPK DS scheme to date, along with their classical computational complexities. We focus on two primary avenues of attack: key recovery and signature forgery. Further detailed cryptanalysis will be conducted in future works.

\

\

\

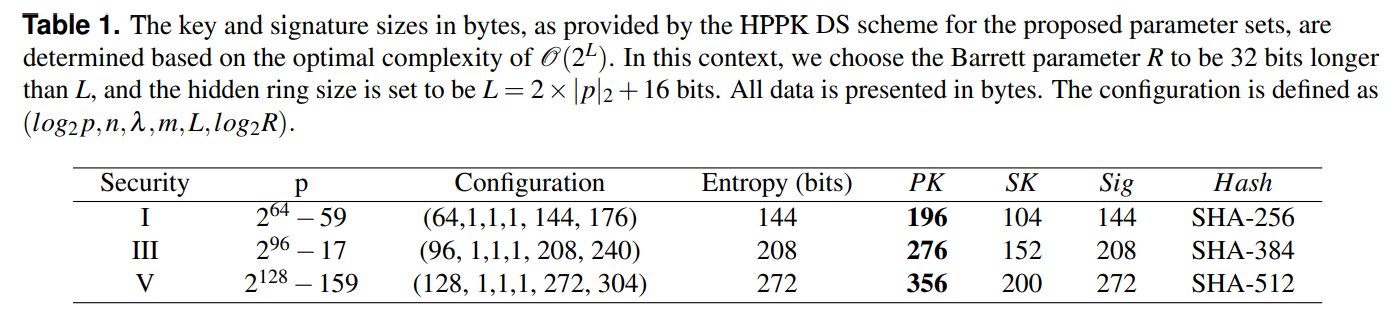
\ Due to the complexity independent from n,λ,m, we could optimally choose n = λ = m = 1. Table 1 presents a comprehensive overview of key sizes, signature sizes, and estimated entropy for all three NIST security levels. HPPK DS ensures robust security with entropy values of 144, 208, and 272 bits for NIST security levels I, III, and V, respectively.

\ The public key (PK) sizes exhibit a linear progression, with dimensions of 196, 276, and 356 bytes for security levels I, III, and V. Conversely, the private key (SK) sizes remain remarkably small, comprising 104 bytes for level I, 152 bytes for level III, and 200 bytes for level V.

\ In terms of signature sizes, HPPK DS maintains efficiency with compact outputs of 144, 208, and 272 bytes for NIST security levels I, III, and V, respectively. Our forthcoming work will delve into the benchmark performance of HPPK DS and provide a thorough comparison with NIST-standardized algorithms.

\

\

7 Conclusion

\

\

References

1. Kuang, R. A deterministic polynomial public key algorithm over a prime galois field gf(p). In 2021 2nd Asia Conference on Computers and Communications (ACCC), 79–88, DOI: 10.1109/ACCC54619.2021.00020 (2021).

   \

2. Evdokimov, S. Factorization of polynomials over finite fields in subexponential time under grh. In International Algorithmic Number Theory Symposium, 209–219 (Springer, 1994).

   \

3. Kuang, R. & Barbeau, M. Performance analysis of the quantum safe multivariate polynomial public key algorithm. In 2021 IEEE International Conference on Quantum Computing and Engineering (QCE), 351–358 (IEEE, 2021).

   \

4. Kuang, R. & Barbeau, M. Indistinguishability and non-deterministic encryption of the quantum safe multivariate polynomial public key cryptographic system. In 2021 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), 1–5 (IEEE, 2021).

   \

5. Kuang, R., Perepechaenko, M. & Barbeau, M. A new post-quantum multivariate polynomial public key encapsulation algorithm. Quantum Inf. Process. 21, 360 (2022).

   \

6. Kuang, R. & Perepechaenko, M. A novel homomorphic polynomial public key encapsulation algorithm [version 1; peer review: awaiting peer review]. F1000Research 12, DOI: 10.12688/f1000research.133031.1 (2023).

   \

7. Kuang, R. & Perepechaenko, M. Homomorphic polynomial public key encapsulation over two hidden rings for quantumsafe key encapsulation. Quantum Inf. Process. 22, 315 (2023).

   \

8. Kuang, R., Perepechaenko, M. & Barbeau, M. A new quantum-safe multivariate polynomial public key digital signature algorithm. Sci. Reports 12, 13168 (2022).

   \

9. Kuang, R. & Perepechaenko, M. Optimization of the multivariate polynomial public key for quantum safe digital signature. Sci. Reports 13, 6363 (2023).

   \

10. Guo, H. An algebraic attack for forging signatures of mppk/ds. Cryptology ePrint Archive, Paper 2023/453 (2023).

    \

11. Merkle, R. & Hellman, M. Hiding information and signatures in trapdoor knapsacks. IEEE Transactions on Inf. Theory 24, 525–530, DOI: 10.1109/TIT.1978.1055927 (1978).

    \

12. Shamir, A. A polynomial time algorithm for breaking the basic merkle-hellman cryptosystem. In 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), 145–152, DOI: 10.1109/SFCS.1982.5 (1982).

    \

13. Nguyen, P. & Stern, J. Merkle-hellman revisited: A cryptanalysis of the qu-vanstone cryptosystem based on group factorizations. In Kaliski, B. S. (ed.) Advances in Cryptology — CRYPTO ’97, 198–212 (Springer Berlin Heidelberg, Berlin, Heidelberg, 1997).

    \

14. Ding, J. & Yang, B.-Y. Multivariate Public Key Cryptography, 193–241 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2009).

    \

15. Chen, L. et al. Report on post-quantum cryptography, vol. 12 (US Department of Commerce, National Institute of Standards and Technology, 2016).

    \

16. Gorjan Alagic and Jacob Alperin-Sheriff and Daniel Apon and David Cooper and Quynh Dang and Yi-Kai Liu and Carl Miller and Dustin Moody and Rene Peralta and Ray Perlner and Angela Robinson and Daniel Smith-Tone. Status report on the first round of the nist post-quantum cryptography standardization process. https://nvlpubs.nist.gov/nistpubs/ir/2019/NIST.IR.8240.pdf (2019).

    \

17. McEliece, R. J. A Public-Key Cryptosystem Based On Algebraic Coding Theory. Deep. Space Netw. Prog. Rep. 44, 114–116 (1978).

    \

18. Avanzi, R. et al. CRYSTALS-KYBER. Tech. rep. available at https://csrc.nist.gov/projects/post-quantumcryptography/round-3-submissions (2020). National Institute of Standards and Technology.

    \

19. Stehle, D. & Steinfeld, R. Making ntruenrypt and ntrusign as secure as standard worst-case problems over ideal lattices. Cryptol. ePrint Arch. Rep. 2013/004 (2013).

    \

20. D’Anvers, J.-P., Karmakar, A., Roy, S. S. & Vercauteren, F. Ml wr-based kem. https://www.esat.kuleuven.be/cosic/pqcrypto/saber/index.html. Online; accessed 1 November 2023.

    \

21. Lyubashevsky, V. et al. CRYSTALS-DILITHIUM. Tech. rep. available at https://csrc.nist.gov/projects/post- quantumcryptography/round-3 submissions (2020). National Institute of Standards and Technology.

    \

22. Prest, T. et al. FALCON. Tech. rep. available at https://csrc.nist.gov/projects/post- quantum-cryptography/round-3- submissions (2020). National Institute of Standards and Technology.

    \

23. Ding, J., Deaton, J., Schmidt, K., Vishakha & Zhang, Z. Cryptanalysis of the lifted unbalanced oil vinegar signature scheme. In Annual International Cryptology Conference, 279–298 (Springer, 2020).

    \

24. NIST. Status report on the second round of the nist post-quantum cryptography standardization process. https://csrc.nist.gov/publications/detail/nistir/8309/final (2021).

    \

25. NIST. Status report on the third round of the nist post-quantum cryptography standardization process. https://csrc.nist.gov/publications/detail/nistir/8413/final (2022).

    \

26. Aumasson, J.-P. et al. SPHINCS+. Tech. rep. available at https://csrc.nist.gov/projects/post- quantum-cryptography/round3-submissions (2020). National Institute of Standards and Technology.

    \

27. Jao, D. & De Feo, L. Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In Yang, B.-Y. (ed.) Post-Quantum Cryptography, 19–34 (Springer Berlin Heidelberg, Berlin, Heidelberg, 2011).

    \

28. Robert, D. Breaking sidh in polynomial time. Cryptology ePrint Archive, Paper 2022/1038 (2022).

    \

29. Castryck, W. & Decru, T. An efficient key recovery attack on sidh (preliminary version). Cryptology ePrint Archive, Paper 2022/975 (2022).

    \

30. Wenger, E., Chen, M., Charton, F. & Lauter, K. Salsa: Attacking lattice cryptography with transformers. Cryptology ePrint Archive, Paper 2022/935 (2022).

    \

31. Li, C. et al. Salsa picante: a machine learning attack on lwe with binary secrets (2023). 2303.04178.

    \

32. Li, C. Y., Wenger, E., Allen-Zhu, Z., Charton, F. & Lauter, K. Salsa verde: a machine learning attack on learning with errors with sparse small secrets (2023). 2306.11641.

    \

33. Sharp, T., Khare, R., Pederson, E. & Traversa, F. L. Scaling up prime factorization with self-organizing gates: A memcomputing approach (2023). 2309.08198.

    \

34. Zhang, Y.-H. & Ventra, M. D. Implementation of digital memcomputing using standard electronic components (2023). 2309.12437.

    \

35. Kuang, R. & Perepechaenko, M. Quantum encryption with quantum permutation pad in ibmq systems. EPJ Quantum Technol. 9, DOI: 10.1140/epjqt/s40507-022-00145-y (2022).

    \

36. Perepechaenko, M. & Kuang, R. Quantum encryption of superposition states with quantum permutation pad in ibm quantum computers. EPJ Quantum Technol. 10, DOI: 10.1140/epjqt/s40507-023-00164-3 (2023).

    \

37. Kuang, R. & Barbeau, M. Quantum permutation pad for universal quantum-safe cryptography. Quantum Inf. Process. 21, 211 (2022).

    \

38. Wikipedia. Barrett reduction (2023).

Acknowledgements

The authors extend their sincere gratitude to Michael Redding and Jay Toth for their continuous support and encouragement in tackling the challenges posed by forgery attacks in MPPK DS. Special thanks are also extended to Dr. Brian LaMacchia for engaging discussions throughout the evolution of HPPK DS developments. Additionally, we want to express our appreciation to one of the reviewers for bringing up the Merkle-Hellman knapsack cryptosystems, from which HPPK cryptography inherits its modular multiplication encryption.

Author contributions statement

R.K conceptualized the extension of HPPK KEM for the digital signature scheme and revised the manuscript based on reviewers’ comments, M.P. conducted the security analysis, and M.S. and D.L. delved into the proposal and its security aspects. All authors contributed to and reviewed the manuscript.

\ The corresponding author is responsible for submitting a competing interests statement on behalf of all authors of the paper. This statement must be included in the submitted article file.

\ Data Availability — All data generated or analyzed during this study is included in this published article.

\

:::info Authors:

(1) Randy Kuang, Quantropi Inc., Ottawa, K1Z 8P9, Canada (randy.kuang@quantropi.com);

(2) Maria Perepechaenko, Quantropi Inc., Ottawa, K1Z 8P9, Canada;

(3) Mahmoud Sayed, Systems and Computer Engineering, Carleton University, Ottawa, K1S 5B6, Canada;

(4) Dafu Lou, Quantropi Inc., Ottawa, K1Z 8P9, Canada.

:::

:::info This paper is available on arxiv under ATTRIBUTION-NONCOMMERCIAL-SHAREALIKE 4.0 INTERNATIONAL license.

:::

\n