Can Light Solve Problems Faster Than Supercomputers?

:::info Authors:

(1) Richard Zhipeng Wang, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom;

(2) James S. Cummins, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom;

(3) Marvin Syed, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom;

(4) Nikita Stroev, Department of Physics of Complex Systems, Weizmann Institute of Science, Rehovot 76100, Israel;

(5) George Pastras, QUBITECH, Thessalias 8, Chalandri, GR 15231 Athens, Greece;

(6) Jason Sakellariou, QUBITECH, Thessalias 8, Chalandri, GR 15231 Athens, Greece;

(7) Symeon Tsintzos, QUBITECH, Thessalias 8, Chalandri, GR 15231 Athens, Greece and UBITECH ltd, 95B Archiepiskopou Makariou, CY 3020 Limassol, Cyprus;

(8) Alexis Askitopoulos, QUBITECH, Thessalias 8, Chalandri, GR 15231 Athens, Greece and UBITECH ltd, 95B Archiepiskopou Makariou, CY 3020 Limassol, Cyprus;

(9) Daniele Veraldi, Department of Physics, University Sapienza, Piazzale Aldo Moro 5, Rome 00185, Italy;

(10) Marcello Calvanese Strinati, Research Center Enrico Fermi, Via Panisperna 89A, 00185 Rome, Italy;

(11) Silvia Gentilini, Institute for Complex Systems, National Research Council (ISC-CNR), Via dei Taurini 19, 00185 Rome, Italy;

(12) Calvanese Strinati, Research Center Enrico Fermi, Via Panisperna 89A, 00185 Rome, Italy

(13) Davide Pierangeli, Institute for Complex Systems, National Research Council (ISC-CNR), Via dei Taurini 19, 00185 Rome, Italy;

(14) Claudio Conti, Department of Physics, University Sapienza, Piazzale Aldo Moro 5, Rome 00185, Italy;

(15) Natalia G. Berlof, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, United Kingdom (N.G.Berloff@damtp.cam.ac.uk).

:::

Table of Links

I. Introduction

II. Spim Performance, Advantages and Generality

III. Inherently Low Rank Problems

A. Properties of Low Rank Graphs

B. Weakly NP-Complete Problems and Hardware Precision Limitation

C. Limitation of Low Rank Matrix Mapping

IV. Low Rank Approximation

A. Decomposition of Target Coupling Matrix

B. How Fields Influence Ran

C. Low Rank Approximation of Coupling Matrices

D. Low-Rank Approximation of Random Coupling Matrices

E. Low Rank Approximation for Portfolio Optimization

F. Low-Rank Matrices in Restricted Boltzmann Machines

V. Constrained Number Partitioning Problem

A. Definition and Characteristics of the Constrained Number Partitioning Problem

B. Computational Hardness of Random CNP Instances

VI. Translation Invariant Problems

A. “Realistic” Spin Glass

B. Circulant Graphs

VII. Conclusions, Acknowledgements, and References

\ We explore the potential of spatial-photonic Ising machines (SPIMs) to address computationally intensive Ising problems that employ low-rank and circulant coupling matrices. Our results indicate that the performance of SPIMs is critically affected by the rank and precision of the coupling matrices. By developing and assessing advanced decomposition techniques, we expand the range of problems SPIMs can solve, overcoming the limitations of traditional Mattis-type matrices. Our approach accommodates a diverse array of coupling matrices, including those with inherently low ranks, applicable to complex NP-complete problems. We explore the practical benefits of low-rank approximation in optimization tasks, particularly in financial optimization, to demonstrate the realworld applications of SPIMs. Finally, we evaluate the computational limitations imposed by SPIM hardware precision and suggest strategies to optimize the performance of these systems within these constraints.

I. INTRODUCTION

The demand for computational power to solve largescale optimization problems is continually increasing in fields such as synthetic biology [1], drug discovery [2], machine learning [3], and materials science [4, 5]. However, many optimization problems of practical interest are NPhard, meaning the resources required to solve them grow exponentially with problem size [6]. At the same time, artificial intelligence systems, including large language models with a rapidly increasing number of parameters, are leading to unsustainable growth in power consumption at data centers [7]. This has spurred interest in analog physical devices that can address these computational challenges with far greater power efficiency than classical computers. Various physical platforms are being explored, including exciton-polariton condensates [8–12], lasers [13–15], and degenerate optical parametric oscillators [16–18]. Many of these platforms are known as Ising machines, which aim to solve an optimization problem called the Ising problem by minimizing the Ising Hamiltonian:

\

\ Ising machines based on spatial light modulators (SLMs) have shown their effectiveness in finding the ground state of Ising Hamiltonians, mainly due to their scalability [20]. However, current experimental implementations of spatial-photonic Ising machines (SPIMs) primarily use Mattis-type coupling matrices [20–22]. The Mattis-type matrix J is defined as the outer product of two identical vectors:

\

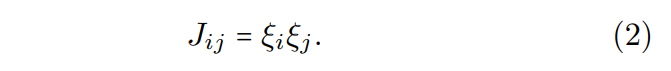
\ This formulation results in a rank-1 matrix with N degrees of freedom, where N is the dimensionality of the vector ξ. Typically, the coupling matrix of an Ising Hamiltonian can be any real symmetric matrix with zeros on its diagonal, encompassing up to N(N − 1)/2 degrees of freedom and a rank that does not exceed N. This restriction significantly limits the variety of Ising Hamiltonians that SPIMs can effectively realize.

\

\ where G(i − j) can be arbitrary function. The Ising Hamiltonian can be effectively evaluated using the correlation function method by calculating the correlation function of measured intensity values from SPIM against a distribution function g, derived via the inverse Fourier transform of the function G(i − j). While this method broadens the range of matrices that can be represented, it introduces a limitation: the dependency of the additional factor G solely on the difference between spin indices i−j restricts output to circulant matrices. Consequently, this method can only represent Ising problems with periodic geometrical properties.

\ The linear combination method, on the other hand, theoretically allows for the representation of arbitrary matrices. This is achieved by decomposing the required coupling matrix into a linear combination of Mattis-type matrices:

\

\ This paper identifies computationally significant problems suitable for efficient implementation on SPIM hardware or other hardware with similar coupling matrix limitations. Many NP-complete problems have already been mapped to Ising models [26]; however, for effective implementation on SPIMs, these Ising models must have coupling matrices that are either low-rank or circulant. In Section II, we discuss the energy efficiency of SPIMs that can be utilized in unconventional hardware for optimization and machine learning applications. In Section III, we explore problems corresponding to Ising models with inherently low-rank coupling matrices and discuss the practical limitations of such models due to the increasing precision requirements of SPIM hardware. In Section IV, we examine the feasibility of finding approximate solutions to computational challenges by approximating them with low-rank Ising models. Notably, a practical optimization problem in finance is well approximated by this approach, allowing for efficient SPIM implementation. The potential applicability of low-rank matrices implementing a restricted Boltzmann machine on SPIM hardware is also briefly discussed. Section V introduces a new variant of an NP-hard problem, the constrained number partitioning (CNP) problem, highlighting its potential to achieve computational hardness with only a slowly increasing precision requirement, enabling existing SPIM hardware to address moderately sized hard problems even with limited precision. Finally, Section VI addresses translationally invariant problems that can be effectively resolved using the correlation function method with SPIMs [24].

\ The following section discusses SPIMs’ performance metrics and inherent advantages, highlighting their potential across various computational tasks.

\

II. SPIM PERFORMANCE, ADVANTAGES AND GENERALITY

By exploiting the properties of light, such as interference and diffraction, SPIMs and other SLM-based devices perform computations in parallel, providing significant speed advantages over electronic systems.

\ \

\ \ The SPIM optical device comprises a single spatial light modulator, a camera, and a single-mode continuouswave laser. The power consumption of an SLM (model Hamamatsu X15213 series) is 15W. The power consumption of a charge-coupled device camera (model Basler Ace 2R) is 5W. The power consumption of a laser (Thorlabs HeNe HNL210LB) is 10W. Thus, the overall SPIM power consumption is 30W. This can be compared with the 16kW needed to run a D-WAVE system [31].

\ In terms of speed, it has been shown that the runtime for a number partitioning optimization problem with problem size N = 16384 is about 10 minutes, which is comparable to the D-WAVE 5000+ Advantage system at N = 121. These comparisons underscore the importance of developing optical annealers based on spatial light modulation [29].

\ Although this paper focuses on SPIMs, the results apply to other alternative analog Ising machines that use similar methods of generating coupling matrices. Specifically, these machines may also employ SLM and techniques that allow the realization of low-rank interaction matrices through the direct implementation of rank-one matrices or the linear combination of multiple rank-one matrices. The problems we discuss in our paper extend their applicability to various analog computational platforms that share these experimental foundations.

\ Having established SPIMs’ general performance and benefits, we now focus on a critical subset of problems—those characterized by inherently low-rank structures.

\

:::info This paper is available on arxiv under CC BY 4.0 DEED license.

:::

\