Comment Toto Réimagine l'Attention Multi-Têtes pour les Prévisions Multivariées

Table des liens

1. Contexte
2. Énoncé du problème
3. Architecture du modèle
4. Données d'entraînement
5. Résultats
6. Conclusions
7. Déclaration d'impact
8. Orientations futures
9. Contributions
10. Remerciements et références

Annexe

3 Architecture du modèle

Toto est un modèle de prévision décodeur uniquement. Ce modèle utilise de nombreuses techniques récentes de la littérature et introduit une nouvelle méthode pour adapter l'attention multi-têtes aux données de séries temporelles multivariées (Fig. 1).

\ 3.1 Conception du Transformer

\ Les modèles Transformer pour la prévision de séries temporelles ont utilisé diverses architectures : encodeur-décodeur [12, 13, 21], encodeur uniquement [14, 15, 17], et décodeur uniquement [19, 23]. Pour Toto, nous utilisons une architecture décodeur uniquement. Les architectures de décodeur ont démontré leur capacité à bien évoluer [25, 26] et permettent des horizons de prédiction arbitraires. La tâche de prédiction causale du prochain patch simplifie également le processus de pré-entraînement.

\ Nous utilisons des techniques issues des architectures les plus récentes de grands modèles de langage (LLM), notamment la pré-normalisation [27], RMSNorm [28], et les couches feed-forward SwiGLU [29].

\ 3.2 Embedding d'entrée

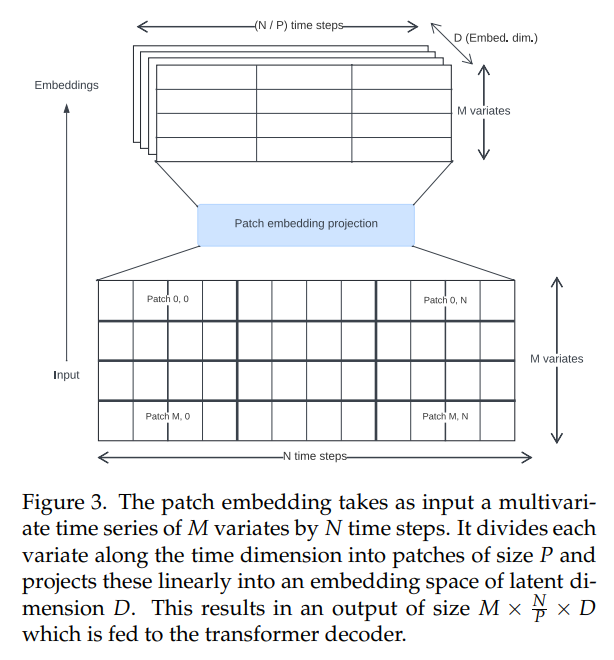
\ Les transformers de séries temporelles dans la littérature ont utilisé diverses approches pour créer des embeddings d'entrée. Nous utilisons des projections de patchs non chevauchants (Fig. 3), introduites pour la première fois pour les Vision Transformers [30, 31] et popularisées dans le contexte des séries temporelles par PatchTST [14]. Toto a été entraîné en utilisant une taille de patch fixe de 32.

\

\ 3.3 Mécanisme d'attention

\ Les métriques d'observabilité sont souvent des séries temporelles multivariées à haute cardinalité. Par conséquent, un modèle idéal gérera nativement les prévisions multivariées. Il devrait pouvoir analyser les relations à la fois dans la dimension temporelle (ce que nous appelons interactions "time-wise") et dans la dimension des canaux (ce que nous appelons interactions "space-wise", suivant la convention de la plateforme Datadog qui décrit différents groupes ou ensembles de tags d'une métrique comme la dimension "espace").

\ Afin de modéliser les interactions spatiales et temporelles, nous devons adapter l'architecture d'attention multi-têtes traditionnelle [11] d'une à deux dimensions. Plusieurs approches ont été proposées dans la littérature pour ce faire, notamment :

\ • Supposer l'indépendance des canaux et calculer l'attention uniquement dans la dimension temporelle [14]. C'est efficace, mais élimine toutes les informations sur les interactions spatiales.

\ • Calculer l'attention uniquement dans la dimension spatiale et utiliser un réseau feed-forward dans la dimension temporelle [17, 18].

\ • Concaténer les variantes le long de la dimension temporelle et calculer une attention croisée complète entre chaque emplacement espace/temps [15]. Cela peut capturer toutes les interactions possibles d'espace et de temps, mais c'est coûteux en calcul.

\ • Calculer une "attention factorisée", où chaque bloc transformer contient un calcul d'attention spatiale et temporelle séparé [16, 32, 33]. Cela permet à la fois le mélange spatial et temporel, et est plus efficace que l'attention croisée complète. Cependant, cela double la profondeur effective du réseau.

\ Pour concevoir notre mécanisme d'attention, nous suivons l'intuition que pour de nombreuses séries temporelles, les relations temporelles sont plus importantes ou prédictives que les relations spatiales. Comme preuve, nous observons que même les modèles qui ignorent complètement les relations spatiales (comme PatchTST [14] et TimesFM [19]) peuvent encore atteindre des performances compétitives sur des ensembles de données multivariés. Cependant, d'autres études (par exemple Moirai [15]) ont montré par des ablations qu'il y a un avantage clair à inclure des relations spatiales.

\ Nous proposons donc une nouvelle variante d'attention factorisée, que nous appelons "Attention Espace-Temps Factorisée Proportionnelle". Nous utilisons un mélange de blocs d'attention alternant entre spatial et temporel. En tant qu'hyperparamètre configurable, nous pouvons modifier le ratio de blocs temporels par rapport aux blocs spatiaux, nous permettant ainsi de consacrer plus ou moins de budget de calcul à chaque type d'attention. Pour notre modèle de base, nous avons sélectionné une configuration avec un bloc d'attention spatiale pour deux blocs temporels.

\ Dans les blocs d'attention temporelle, nous utilisons un masquage causal et des embeddings positionnels rotatifs [34] avec XPOS [35] afin de modéliser de manière autorégressive les caractéristiques dépendantes du temps. Dans les blocs spatiaux, en revanche, nous utilisons une attention bidirectionnelle complète afin de préserver l'invariance de permutation des covariables, avec un masque d'ID en bloc diagonal pour garantir que seules les variantes liées s'attendent mutuellement. Ce masquage nous permet de regrouper plusieurs séries temporelles multivariées indépendantes dans le même lot, afin d'améliorer l'efficacité de l'entraînement et de réduire la quantité de remplissage.

\ 3.4 Tête de prédiction probabiliste

\ Pour être utile dans les applications de prévision, un modèle doit produire des prédictions probabilistes. Une pratique courante dans les modèles de séries temporelles consiste à utiliser une couche de sortie où le modèle régresse les paramètres d'une distribution de probabilité. Cela permet de calculer des intervalles de prédiction en utilisant l'échantillonnage de Monte Carlo [7].

\ Les choix courants pour une couche de sortie sont Normal [7] et Student-T [23, 36], qui peuvent améliorer la robustesse aux valeurs aberrantes. Moirai [15] permet des distributions résiduelles plus flexibles en proposant un nouveau modèle de mélange incorporant une combinaison pondérée de sorties gaussiennes, Student-T, Log-normales et binomiales négatives.

\ Cependant, les séries temporelles du monde réel peuvent souvent avoir des distributions complexes difficiles à ajuster, avec des valeurs aberrantes, des queues lourdes, une asymétrie extrême et une multimodalité. Afin de s'adapter à ces scénarios, nous introduisons une vraisemblance de sortie encore plus flexible. Pour ce faire, nous employons une méthode basée sur les modèles de mélange gaussien (GMMs), qui peuvent approximer n'importe quelle fonction de densité ([37]). Pour éviter l'instabilité d'entraînement en présence de valeurs aberrantes, nous utilisons un modèle de mélange Student-T (SMM), une généralisation robuste des GMMs [38] qui a déjà montré des promesses pour la modélisation de séries temporelles financières à queue lourde [39, 40]. Le modèle prédit k distributions Student-T (où k est un hyperparamètre) pour chaque pas de temps, ainsi qu'une pondération apprise.

\

\ Lorsque nous effectuons l'inférence, nous tirons des échantillons de la distribution de mélange à chaque horodatage, puis nous réinjectons chaque échantillon dans le décodeur pour la prédiction suivante. Cela nous permet de produire des intervalles de prédiction à n'importe quel quantile, limités uniquement par le nombre d'échantillons ; pour des queues plus précises, nous pouvons choisir de consacrer plus de calcul à l'échantillonnage (Fig. 2).

\ 3.5 Mise à l'échelle entrée/sortie

\ Comme dans d'autres modèles de séries temporelles, nous effectuons une normalisation d'instance sur les données d'entrée avant de les faire passer par l'embedding de patch, afin que le modèle généralise mieux aux entrées de différentes échelles [41]. Nous mettons à l'échelle les entrées pour avoir une moyenne nulle et un écart-type unitaire. Les prédictions de sortie sont ensuite remises à l'échelle aux unités d'origine.

\ 3.6 Objectif d'entraînement

\ En tant que modèle décodeur uniquement, Toto est pré-entraîné sur la tâche de prédiction du prochain patch. Nous minimisons la log-vraisemblance négative du prochain patch prédit par rapport à la sortie de distribution du modèle. Nous entraînons le modèle en utilisant l'optimiseur AdamW [42].

\ 3.7 Hyperparamètres

\ Les hyperparamètres utilisés pour Toto sont détaillés dans le Tableau A.1, avec un total de 103 millions de paramètres.

\

:::info Auteurs :

(1) Ben Cohen (ben.cohen@datadoghq.com) ;

(2) Emaad Khwaja (emaad@datadoghq.com) ;

(3) Kan Wang (kan.wang@datadoghq.com) ;

(4) Charles Masson (charles.masson@datadoghq.com) ;

(5) Elise Rame (elise.rame@datadoghq.com) ;

(6) Youssef Doubli (youssef.doubli@datadoghq.com) ;

(7) Othmane Abou-Amal (othmane@datadoghq.com).

:::

:::info Cet article est disponible sur arxiv sous licence CC BY 4.0.

:::

\