Pas de gagnants ici : Pourquoi chaque enchère "équitable" de crypto finit par être triviale

Table des Liens

Abstrait et 1. Introduction

1.1 Aperçu Technique

1.2 Travaux Connexes

1. Modèle et Préliminaires et 2.1 Mécanismes de Frais de Transaction

   2.2 Les Desiderata TFM

2. Comprendre OCA

   3.1 La Différence Entre SCP et OCA

   3.2 Résultats Préliminaires Utiles pour les TFM à l'épreuve d'OCA

3. Mécanismes Déterministes à l'épreuve d'OCA

4. Mécanismes Randomisés à l'épreuve d'OCA

5. Discussion et Références

   \

A. Preuves Manquantes

B. Mécanismes Déterministes Non-anonymes

4 Mécanismes Déterministes à l'épreuve d'OCA

L'exemple 3.6 montre que généralement, les propriétés DSIC et 1-OCA-proofness ne suffisent pas à garantir un revenu nul. Nous montrons maintenant que pour les mécanismes déterministes, l'ajout de la propriété MMIC suffit pour obtenir un résultat général de revenu 0.

\ Théorème 4.1. Tout mécanisme déterministe DSIC+MMIC+1-OCA-proof a un revenu minier de 0.

\

\ Cependant, nous pouvons fournir une caractérisation significative même en supprimant la condition DSIC. La caractérisation, donnée dans le Lemme 4.3, reste très similaire, bien qu'avec plus de liberté pour décider de la règle de paiement.

\

\ Nous concluons que la combustion pour toutes les valeurs allouées est une constante R. Nous comparons maintenant R avec le r que nous avons pour la règle d'allocation.

\ Nous concluons que R = r, ce qui donne la caractérisation spécifiée.

\ Cela nous permet de caractériser davantage les règles d'allocation et de combustion plus généralement, pour les mécanismes déterministes 1-OCA-proof.

\ Lemme 4.4. Tout mécanisme déterministe 1-OCA-proof a, p, β est exactement de la forme suivante : Pour un certain r ≥ 0, le mécanisme attribue l'article à l'enchérisseur le plus élevé à condition qu'il ait une valeur supérieure à r, ou n'attribue pas l'article du tout. Lorsqu'il est attribué, la combustion est exactement r. C'est-à-dire,

\

\

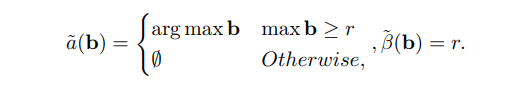
\ Nous pouvons maintenant caractériser précisément deux classes de mécanismes : La classe des mécanismes déterministes DSIC+1-OCA-proof, et la classe des mécanismes déterministes MMIC+1-OCA-proof.

\

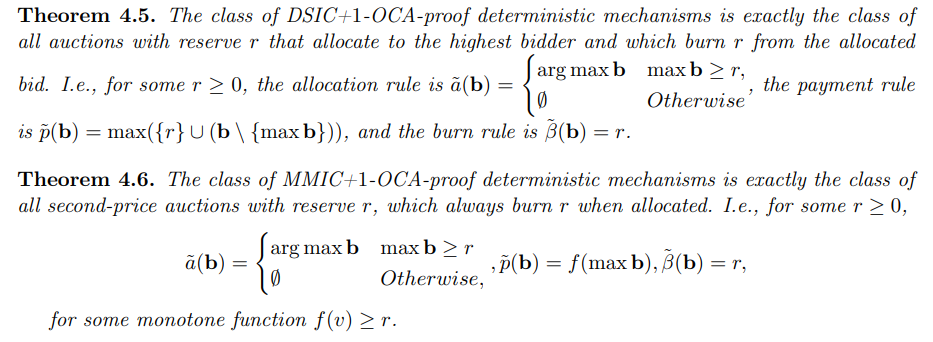
\ Ces caractérisations précises nous permettent maintenant de conclure avec ce qui suit :

Théorème 4.7. Ne jamais attribuer l'article est le seul mécanisme déterministe DSIC+MMIC+1-OCA-proof.

\ Preuve. Cela découle du Théorème 4.5 et du Théorème 4.6, car les deux classes caractérisées dans ces résultats n'ont que le mécanisme trivial en commun (en prenant r = ∞). Pour voir cela intuitivement, considérez la classe des enchères au second prix avec réserve r et combustion constante r du Théorème 4.5. Les enchères au second prix ne sont pas MMIC car le mineur peut ajouter un enchérisseur fictif arbitrairement proche de l'enchère gagnante pour augmenter le paiement.

\

5 Mécanismes Randomisés à l'épreuve d'OCA

Nous étendons maintenant la discussion aux mécanismes randomisés à l'épreuve d'OCA. Pour les mécanismes randomisés, nous considérons la notion plus forte d'OCA-proofness (plutôt que 1-OCA-proofness). Nous le faisons pour éviter l'encombrement dans les définitions, car dans les mécanismes randomisés, la coalition gagnante peut très bien nécessairement inclure tous les enchérisseurs (car chacun a une probabilité fractionnaire de gagner).

\ Nous considérons maintenant une propriété naturelle pour les mécanismes :

\ Corollaire 5.4. Par le Lemme 5.3, un mécanisme invariant d'échelle DSIC+OCA-proof ne brûle pas de frais (c'est-à-dire que sa règle de combustion est la fonction constante zéro), tandis que du Lemme 3.5, nous obtenons qu'un mécanisme DSIC+MMIC+OCAproof a des paiements égaux à la combustion dans le cas d'un seul enchérisseur. Par conséquent, nous devons avoir 0 paiement dans le cas d'un seul enchérisseur, et donc, dans le cas d'un seul enchérisseur, l'article est soit toujours attribué, soit jamais attribué.

\ Lemme 5.5. Pour un mécanisme DSIC+MMIC+OCA-proof, si l'article est toujours ou jamais attribué dans le cas d'un seul enchérisseur, le mécanisme doit être trivial.

\

\ Ainsi, comme résultat direct du Corollaire 5.4 et du Lemme 5.5, nous avons :

Corollaire 5.6. Il n'existe pas de mécanisme non trivial invariant d'échelle DSIC+MMIC+OCA-proof.

\ L'argument que nous utilisons dans le Lemme 5.5 peut être étendu pour nous permettre également d'exclure la classe des enchères qui satisfont une propriété que nous appelons probabilité totale constante d'allocation (CTPA), qui est définie dans la Déf. 5.7. C'est une classe intéressante d'enchères, car elle inclut toutes les enchères efficaces (qui font partie de la classe de probabilité totale constante 1 d'allocation), y compris les enchères au premier prix et au second prix.

\

\

\

\ et donc par l'équation de faisabilité (1) :

\ Notez que c'est le côté gauche du Lemme 5.12 où nous considérons les enchères B · b, A · b. Nous pouvons donc répéter la façon dont nous avons développé l'Eq. (14) (pour le cas des enchères A · b, A · b) et, en considérant que le mineur omet l'enchère B · b, obtenir :

\ De plus, pour le cas de deux enchérisseurs, nous pouvons montrer une limite supérieure et inférieure utile sur la façon dont la fonction devrait "favoriser" l'enchérisseur le plus élevé :

\

\

\

\

:::info Auteurs :

(1) Yotam Gafni, Institut Weizmann (yotam.gafni@gmail.com);

(2) Aviv Yaish, L'Université Hébraïque, Jérusalem (aviv.yaish@mail.huji.ac.il).

:::

:::info Cet article est disponible sur arxiv sous licence CC BY 4.0 DEED.

:::

\