Propagateurs Holographiques : Géodésiques et Criticité Locale

Table des liens

• Prologue
• Règles diagrammatiques
• Eikonal direct
• Bosonisation héritée
• Holographie Wonton
• Propagateurs holographiques
• Cuprates étranges
• Choses plus étranges
• Épilogue

Propagateurs holographiques

Les premières études holographiques des propagateurs de fermions [28] ont produit un certain nombre de résultats intrigants, notamment des surfaces de Fermi multiples (qui fusionnent en une 'boule de Fermi' critique dans certaines limites extrêmes), des pôles sans dispersion, et une dépendance oscillatoire en fréquence (dont il a été démontré plus tard qu'elle n'apparaît pas dans des constructions 'top down' plus systématiques [26]), etc. Une interprétation physique de ces résultats est entravée par le fait qu'une grande partie de ce travail est numérique.

\ Un calcul semi-classique simple et propice au traitement analytique peut être effectué dans le régime mL ≫ 1 où m est une masse du fermion dual en volume conjecturé [28, 29]. Dans ce régime, les chemins du fermion contribuant à diverses amplitudes quantiques suivent de près les trajectoires classiques de frontière à frontière (géodésiques) dérivées de l'action (en temps imaginaire)

\

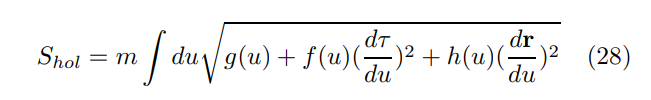
\ en variant τ(u) et r(u).

\ En évaluant cette action sur sa géodésique, on obtient

\

\ Bien qu'un calcul analytique explicite de (29) ne puisse être effectué que dans certains cas particuliers, les dépendances espace/temps à un paramètre peuvent être facilement trouvées pour une grande variété de métriques. Spécifiquement, pour la métrique HV (26), on obtient [29, 30]

\

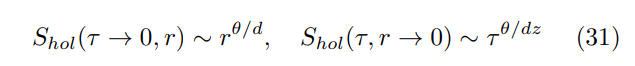
\ Notamment, en l'absence de violation d'hyperscaling (θ = 0), ces deux asymptotiques deviennent soit constantes (moins probable) soit logarithmiques (plus probable, voir ci-dessous). Ainsi, si le Lagrangien EMD classique (22) devait représenter un dual en volume valide d'une théorie de frontière avec l'interaction de type jauge (1), les asymptotiques (31) ne seraient pas facilement conciliables avec les résultats d'eikonal/bosonisation (11,21) qui dépendent principalement de z (via η) plutôt que de θ.

\

\ et est composé des deux solutions indépendantes qui se lisent

\

\ En imposant les conditions aux limites appropriées et en suivant le dictionnaire holographique [26], on définit alors le propagateur comme un coefficient de réflexion pour l'onde incidente à la frontière

\

\ Un comportement différent (inaccessible dans le cas d'une métrique HV (26) avec z et θ finis) se produit pour α = β + 1, auquel cas l'intégrale dans (33) diverge à u → 0. Ce régime NFL particulier, appelé 'criticité locale', est caractérisé par le propagateur

\

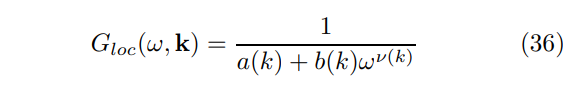
\ où a(k), b(k), et ν(k) ∼ k sont des fonctions non singulières de l'impulsion qui peuvent, en général, produire de multiples pôles identifiés comme les FS distinctes ('fractionnées') [28].

\ La transformation de Fourier de (36) est compliquée par le fait que G(ω, k) n'est pas analytiquement connu sur toute la gamme de ses arguments. Cependant, la transformation de Fourier rapide (et/ou furieuse) via un point de selle suggère la forme suivante de cette fonction dans le domaine spatio-temporel

\

\ Ajoutant à l'intrigue, il y a des résultats récents de Monte Carlo sur les modèles Hubbard 2d et t − J qui ont longtemps été considérés comme représentant l'état normal NFL prototypique dans les cuprates. Ces résultats ne se conforment pas facilement à une fonction d'auto-énergie indépendante de l'impulsion, mais fortement dépendante de l'énergie, montrant moins de dépendance à l'énergie/température que n'importe laquelle des expressions ci-dessus [33]. Il reste à voir ce que cela pourrait impliquer pour l'applicabilité générale des théories des fermions ('spinons') régis par les interactions (1) à l'analyse de ces modèles microscopiques.

\

:::info Auteur :

(1) D. V. Khveshchenko, Département de Physique et d'Astronomie, Université de Caroline du Nord, Chapel Hill, NC 27599.

:::

:::info Cet article est disponible sur arxiv sous licence CC BY 4.0 DEED.

:::

\