Performance de l'optimisation sur les plongements gaussiens synthétiques et arborescents

Table des liens

Résumé et 1. Introduction

1. Travaux connexes

2. Techniques de relaxation convexe pour les SVM hyperboliques

   3.1 Préliminaires

   3.2 Formulation originale du HSVM

   3.3 Formulation semi-définie

   3.4 Relaxation Moment-Somme des carrés

3. Expériences

   4.1 Jeu de données synthétique

   4.2 Jeu de données réel

4. Discussions, Remerciements et Références

   \

A. Preuves

B. Extraction de solution dans la formulation relaxée

C. Sur la hiérarchie de relaxation Moment Somme des carrés

D. Calibration de Platt [31]

E. Résultats expérimentaux détaillés

F. Machine à vecteurs de support hyperbolique robuste

4.1 Jeu de données synthétique

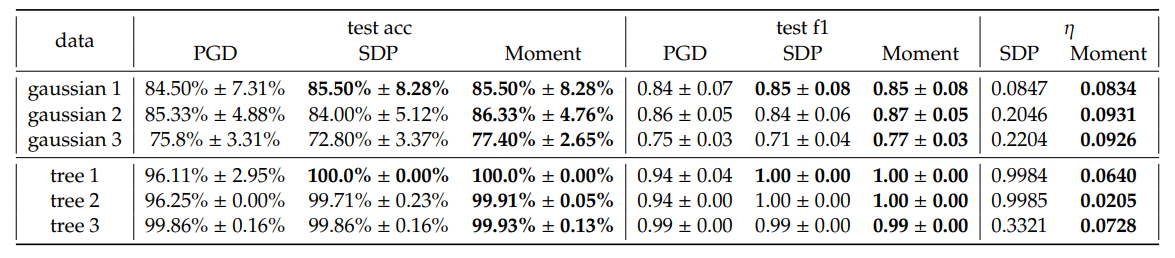
\ En général, nous observons un léger gain en précision de test moyenne et en score F1 pondéré de SDP et Moment par rapport à PGD. Notamment, nous observons que Moment montre souvent des améliorations plus cohérentes par rapport à SDP, dans la plupart des configurations. De plus, Moment donne des écarts d'optimalité 𝜂 plus petits que SDP. Cela correspond à notre attente que Moment est plus serré que le SDP.

\ Bien que dans certains cas, par exemple lorsque 𝐾 = 5, Moment atteint des pertes significativement plus faibles par rapport à PGD et SDP, ce n'est généralement pas le cas. Nous soulignons que ces pertes ne sont pas des mesures directes de la généralisabilité des séparateurs hyperboliques à marge maximale ; elles sont plutôt des combinaisons de maximisation de marge et de pénalisation pour la mauvaise classification qui évolue avec 𝐶. Par conséquent, l'observation que la performance en précision de test et en score F1 pondéré est meilleure, même si la perte calculée en utilisant les solutions extraites de SDP et Moment est parfois plus élevée que celle de PGD, pourrait être due au paysage de perte complexe. Plus précisément, les augmentations observées de la perte peuvent être attribuées aux subtilités du paysage plutôt qu'à l'efficacité des méthodes d'optimisation. Sur la base des résultats de précision et de score F1, empiriquement, les méthodes SDP et Moment identifient des solutions qui se généralisent mieux que celles obtenues en exécutant uniquement la descente de gradient. Nous fournissons une analyse plus détaillée sur l'effet des hyperparamètres dans l'Annexe E.2 et le temps d'exécution dans le Tableau 4. La frontière de décision pour Gaussian 1 est visualisée dans la Figure 5.

\

\ Plongement d'arbre synthétique. Comme les espaces hyperboliques sont adaptés au plongement d'arbres, nous générons des graphes d'arbres aléatoires et les plongeons dans H2 en suivant Mishne et al. [6]. Plus précisément, nous étiquetons les nœuds comme positifs s'ils sont des enfants d'un nœud spécifié et négatifs sinon. Nos modèles sont ensuite évalués pour la classification de sous-arbres, visant à identifier une frontière qui inclut tous les nœuds enfants au sein du même sous-arbre. Une telle tâche a diverses applications pratiques. Par exemple, si l'arbre représente un ensemble de jetons, la frontière de décision peut mettre en évidence des régions sémantiques dans l'espace hyperbolique qui correspondent aux sous-arbres du graphe de données. Nous soulignons qu'une caractéristique commune dans une telle tâche de classification de sous-arbres est le déséquilibre des données, qui conduit généralement à une mauvaise généralisabilité. Par conséquent, nous visons à utiliser cette tâche pour évaluer les performances de nos méthodes dans ce contexte difficile. Trois plongements sont sélectionnés et visualisés dans la Figure 3 et les performances sont résumées dans le Tableau 1. Le temps d'exécution des arbres sélectionnés se trouve dans le Tableau 4. La frontière de décision de l'arbre 2 est visualisée dans la Figure 6.

\ Similaire aux résultats des jeux de données gaussiens synthétiques, nous observons de meilleures performances de SDP et Moment par rapport à PGD, et en raison du déséquilibre des données avec lequel les méthodes GD ont généralement du mal, nous avons un gain plus important en score F1 pondéré dans ce cas. De plus, nous observons de grands écarts d'optimalité pour SDP mais un écart très serré pour Moment, certifiant l'optimalité de Moment même lorsque le déséquilibre de classe est sévère.

\

\

:::info Auteurs :

(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (shengyang@g.harvard.edu) ;

(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (peihanliu@fas.harvard.edu) ;

(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, et Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA (cpehlevan@seas.harvard.edu).

:::

:::info Cet article est disponible sur arxiv sous licence CC by-SA 4.0 Deed (Attribution-Partage dans les mêmes conditions 4.0 International).

:::

\