सिंथेटिक गॉसियन और ट्री एम्बेडिंग पर ऑप्टिमाइज़ेशन प्रदर्शन

लिंक की तालिका

सार और 1. परिचय

1. संबंधित कार्य

2. हाइपरबोलिक SVMs के लिए उत्तल विश्राम तकनीकें

   3.1 प्रारंभिक बातें

   3.2 HSVM का मूल सूत्रीकरण

   3.3 सेमीडेफिनिट सूत्रीकरण

   3.4 मोमेंट-सम-ऑफ-स्क्वायर्स विश्राम

3. प्रयोग

   4.1 सिंथेटिक डेटासेट

   4.2 वास्तविक डेटासेट

4. चर्चाएं, स्वीकृतियां, और संदर्भ

   \

A. प्रमाण

B. विश्रांत सूत्रीकरण में समाधान निष्कर्षण

C. मोमेंट सम-ऑफ-स्क्वायर्स विश्राम पदानुक्रम पर

D. प्लैट स्केलिंग [31]

E. विस्तृत प्रयोगात्मक परिणाम

F. रोबस्ट हाइपरबोलिक सपोर्ट वेक्टर मशीन

4.1 सिंथेटिक डेटासेट

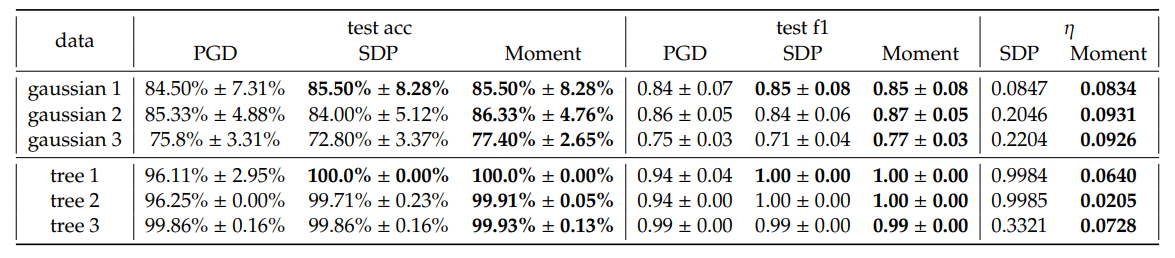
\ सामान्य तौर पर, हम PGD की तुलना में SDP और मोमेंट से औसत परीक्षण सटीकता और भारित F1 स्कोर में एक छोटा लाभ देखते हैं। विशेष रूप से, हम देखते हैं कि अधिकांश कॉन्फ़िगरेशन में SDP की तुलना में मोमेंट अक्सर अधिक सुसंगत सुधार दिखाता है। इसके अलावा, मोमेंट SDP की तुलना में छोटे इष्टतमता अंतर 𝜂 देता है। यह हमारी अपेक्षा से मेल खाता है कि मोमेंट SDP की तुलना में अधिक तंग है।

\ हालांकि कुछ मामलों में, उदाहरण के लिए जब 𝐾 = 5 होता है, मोमेंट PGD और SDP दोनों की तुलना में काफी छोटे नुकसान प्राप्त करता है, यह आमतौर पर ऐसा नहीं होता है। हम जोर देते हैं कि ये नुकसान मैक्स-मार्जिन हाइपरबोलिक सेपरेटर्स की सामान्यीकरण क्षमता के प्रत्यक्ष माप नहीं हैं; बल्कि, वे मार्जिन अधिकतमीकरण और गलत वर्गीकरण के लिए दंड का संयोजन हैं जो 𝐶 के साथ स्केल होता है। इसलिए, यह अवलोकन कि परीक्षण सटीकता और भारित F1 स्कोर में प्रदर्शन बेहतर है, भले ही SDP और मोमेंट से निकाले गए समाधानों का उपयोग करके गणना की गई हानि कभी-कभी PGD से अधिक होती है, जटिल हानि परिदृश्य के कारण हो सकती है। अधिक विशेष रूप से, हानि में देखी गई वृद्धि को अनुकूलन विधियों की प्रभावशीलता के बजाय परिदृश्य की जटिलताओं के लिए जिम्मेदार ठहराया जा सकता है। सटीकता और F1 स्कोर परिणामों के आधार पर, अनुभवजन्य रूप से SDP और मोमेंट विधियां ऐसे समाधानों की पहचान करती हैं जो अकेले ग्रेडिएंट डिसेंट चलाने से प्राप्त समाधानों की तुलना में बेहतर सामान्यीकृत होते हैं। हम परिशिष्ट E.2 में हाइपरपैरामीटर के प्रभाव और तालिका 4 में रनटाइम पर अधिक विस्तृत विश्लेषण प्रदान करते हैं। गॉसियन 1 के लिए निर्णय सीमा चित्र 5 में देखी गई है।

\

\ सिंथेटिक ट्री एम्बेडिंग। चूंकि हाइपरबोलिक स्पेस पेड़ों को एम्बेड करने के लिए अच्छे हैं, हम Mishne et al. [6] के बाद यादृच्छिक ट्री ग्राफ उत्पन्न करते हैं और उन्हें H2 में एम्बेड करते हैं। विशेष रूप से, यदि नोड किसी निर्दिष्ट नोड के बच्चे हैं तो हम उन्हें सकारात्मक के रूप में लेबल करते हैं और अन्यथा नकारात्मक। फिर हमारे मॉडलों का मूल्यांकन सबट्री वर्गीकरण के लिए किया जाता है, जिसका उद्देश्य एक ऐसी सीमा की पहचान करना है जिसमें एक ही सबट्री के भीतर सभी बच्चे नोड शामिल हों। ऐसे कार्य के विभिन्न व्यावहारिक अनुप्रयोग हैं। उदाहरण के लिए, यदि ट्री टोकन के एक सेट का प्रतिनिधित्व करता है, तो निर्णय सीमा हाइपरबोलिक स्पेस में अर्थ संबंधी क्षेत्रों को उजागर कर सकती है जो डेटा ग्राफ के सबट्री से संबंधित हैं। हम जोर देते हैं कि ऐसे सबट्री वर्गीकरण कार्य में एक सामान्य विशेषता डेटा असंतुलन है, जो आमतौर पर खराब सामान्यीकरण क्षमता की ओर ले जाता है। इसलिए, हम इस कठिन परिस्थिति में अपनी विधियों के प्रदर्शन का आकलन करने के लिए इस कार्य का उपयोग करने का लक्ष्य रखते हैं। तीन एम्बेडिंग का चयन किया गया है और चित्र 3 में देखा गया है और प्रदर्शन तालिका 1 में सारांशित है। चयनित पेड़ों का रनटाइम तालिका 4 में पाया जा सकता है। ट्री 2 की निर्णय सीमा चित्र 6 में देखी गई है।

\ सिंथेटिक गॉसियन डेटासेट के परिणामों के समान, हम PGD की तुलना में SDP और मोमेंट से बेहतर प्रदर्शन देखते हैं, और डेटा असंतुलन के कारण जिससे GD विधियां आमतौर पर जूझती हैं, इस मामले में हमें भारित F1 स्कोर में अधिक लाभ मिलता है। इसके अलावा, हम SDP के लिए बड़े इष्टतमता अंतर देखते हैं लेकिन मोमेंट के लिए बहुत तंग अंतर देखते हैं, जो वर्ग-असंतुलन गंभीर होने पर भी मोमेंट की इष्टतमता को प्रमाणित करता है।

\

\

:::info लेखक:

(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (shengyang@g.harvard.edu);

(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (peihanliu@fas.harvard.edu);

(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, और Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA (cpehlevan@seas.harvard.edu)।

:::

:::info यह पेपर arxiv पर उपलब्ध है CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International) लाइसेंस के तहत।

:::

\