Como o WormHole acelera a busca de caminhos em grafos com mil milhões de arestas

Tabela de Links

Abstrato e 1. Introdução

1.1 Nossa Contribuição

1.2 Configuração

1.3 O algoritmo

1. Trabalhos Relacionados

2. Algoritmo

   3.1 A Fase de Decomposição Estrutural

   3.2 A Fase de Roteamento

   3.3 Variantes do WormHole

3. Análise Teórica

   4.1 Preliminares

   4.2 Sublinearidade do Anel Interno

   4.3 Erro de Aproximação

   4.4 Complexidade de Consulta

4. Resultados Experimentais

   5.1 WormHole𝐸, WormHole𝐻 e BiBFS

   5.2 Comparação com métodos baseados em índice

   5.3 WormHole como primitiva: WormHole𝑀

Referências

1.1 Nossa Contribuição

Desenvolvemos um novo algoritmo, WormHole, que cria uma estrutura de dados permitindo-nos responder a múltiplas consultas de caminho mais curto explorando a estrutura típica de muitas redes sociais e de informação. O WormHole é simples, fácil de implementar e teoricamente fundamentado. Fornecemos várias variantes dele, cada uma adequada para um cenário diferente, mostrando excelentes resultados empíricos em uma variedade de conjuntos de dados de rede. Abaixo estão algumas das suas características principais:

\ • Compromisso entre desempenho e precisão. Até onde sabemos, o nosso é o primeiro algoritmo sublinear aproximado de caminhos mais curtos em grandes redes. O facto de permitirmos pequenos erros aditivos dá origem a um compromisso entre tempo/espaço de pré-processamento e tempo por consulta, e permite-nos chegar

\

\ a uma solução com pré-processamento eficiente e tempo rápido por consulta. Notavelmente, nossa variante mais precisa (mas mais lenta), WormHole𝐸, tem precisão quase perfeita: mais de 90% das consultas são respondidas sem erro aditivo, e em todas as redes, mais de 99% das consultas são respondidas com erro aditivo de no máximo 2. Veja a Tabela 3 para mais detalhes.

\ • Tempo de configuração extremamente rápido. Nosso tempo de construção de índice mais longo foi de apenas dois minutos, mesmo para grafos com bilhões de arestas. Para contextualizar, PLL e MLL esgotaram o tempo em metade das redes que testamos, e para grafos de tamanho moderado onde PLL e MLL concluíram suas execuções, a construção do índice WormHole foi 100 vezes mais rápida. Ou seja, o WormHole terminou em segundos enquanto o PLL levou horas. Veja as Tabelas 4 e 5. Este tempo de configuração rápido é alcançado devido ao uso de um índice de tamanho sublinear. Para as maiores redes que consideramos, é suficiente usar um índice de cerca de 1% dos nós para obter um pequeno erro aditivo médio – veja a Tabela 1. Para redes menores, pode ser até 6%.

\ • Tempo de consulta rápido. Comparado ao BiBFS, a versão vanilla WormHole𝐸 (sem otimizações baseadas em índice) é 2 vezes mais rápida para quase todos os grafos e mais de 4 vezes mais rápida nos três maiores grafos que testamos. Uma variante simples, WormHole𝐻, alcança uma melhoria de ordem de magnitude com algum custo para a precisão: consistentemente 20 vezes mais rápida em quase todos os grafos, e mais de 180 vezes para o maior grafo que temos. Veja a Tabela 3 para uma comparação completa. Métodos baseados em indexação tipicamente respondem consultas em microssegundos; ambas as variantes mencionadas ainda estão no regime de milissegundos.

\ • Combinando WormHole e o estado da arte. O WormHole funciona armazenando um pequeno subconjunto de vértices nos quais calculamos os caminhos mais curtos exatos. Para consultas arbitrárias, roteamos nosso caminho através deste subconjunto, que chamamos de núcleo. Usamos esta ideia para fornecer uma terceira variante, WormHole𝑀, implementando o estado da arte para caminhos mais curtos, MLL, no núcleo. Isso alcança tempos de consulta comparáveis ao MLL (com a mesma garantia de precisão que o WormHole𝐻) a uma fração do custo de configuração, e funciona para grafos massivos onde o MLL não termina. Exploramos esta abordagem combinada na seção §5.3 e fornecemos estatísticas na Tabela 6.

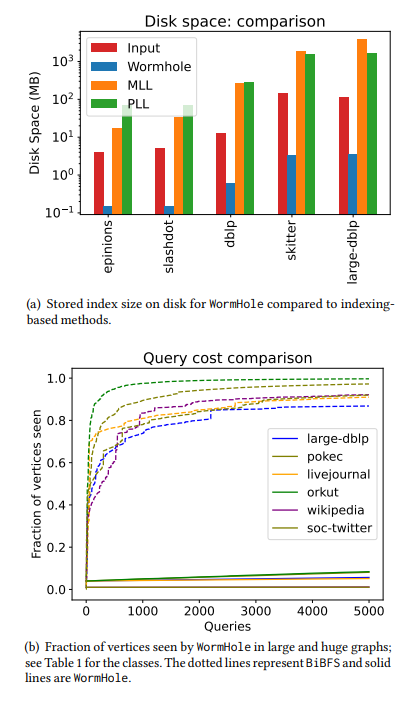
\ • Complexidade de consulta sublinear. A complexidade de consulta refere-se ao número de vértices consultados pelo algoritmo. Em um modelo de acesso de consulta limitado onde consultar um nó revela sua lista de vizinhos (veja §1.2), a complexidade de consulta do nosso algoritmo escala muito bem com o número de consultas de distância/caminho mais curto feitas. Para responder a 5000 consultas aproximadas de caminho mais curto, nosso algoritmo observa apenas entre 1% e 20% dos nós para a maioria das redes. Em comparação, o BiBFS vê mais de 90% do grafo para responder a algumas centenas de consultas de caminho mais curto. Veja as Figuras 2 e 5 para uma comparação.

\ • Garantias comprováveis sobre erro e desempenho. Na seção §4, provamos um conjunto de resultados teóricos complementando e explicando o desempenho empírico. Os resultados, declarados informalmente abaixo, são provados para o modelo Chung-Lu de grafos aleatórios com uma distribuição de grau de lei de potência [15–17].

\ Teorema 1.1 (Informal). Em um grafo aleatório Chung-Lu 𝐺 com expoente de lei de potência 𝛽 ∈ (2,3) em 𝑛 vértices, o WormHole tem as seguintes garantias com alta probabilidade:

\

\

:::info Autores:

(1) Talya Eden, Universidade Bar-Ilan (talyaa01@gmail.com);

(2) Omri Ben-Eliezer, MIT (omrib@mit.edu);

(3) C. Seshadhri, UC Santa Cruz (sesh@ucsc.edu).

:::

:::info Este artigo está disponível no arxiv sob licença CC BY 4.0.

:::

\