Compreendendo o erro de aproximação e a complexidade de consulta no encaminhamento WormHole

Tabela de Links

Abstrato e 1. Introdução

1.1 Nossa Contribuição

1.2 Configuração

1.3 O algoritmo

1. Trabalhos Relacionados

2. Algoritmo

   3.1 A Fase de Decomposição Estrutural

   3.2 A Fase de Roteamento

   3.3 Variantes do WormHole

3. Análise Teórica

   4.1 Preliminares

   4.2 Sublinearidade do Anel Interno

   4.3 Erro de Aproximação

   4.4 Complexidade de Consulta

4. Resultados Experimentais

   5.1 WormHole𝐸, WormHole𝐻 e BiBFS

   5.2 Comparação com métodos baseados em índice

   5.3 WormHole como primitiva: WormHole𝑀

Referências

4.3 Erro de Aproximação

Agora que temos um anel interno sublinear que contém o núcleo Chung-Lu, devemos mostrar que o roteamento de caminhos através dele incorre apenas numa pequena penalidade. Intuitivamente, quanto maior o anel interno, mais fácil é satisfazer isto: se o anel interno for o grafo inteiro, a afirmação é trivialmente verdadeira. Portanto, o desafio está em mostrar que podemos alcançar uma forte garantia em termos de precisão mesmo com um anel interno sublinear. Provamos que o WormHole incorre num erro aditivo de no máximo 𝑂(loglog𝑛) para todos os pares, o que é muito menor que o diâmetro Θ(log𝑛).

\

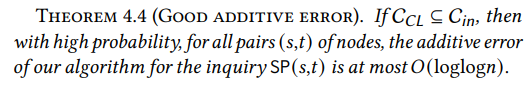
\ O resultado acima mantém-se com alta probabilidade mesmo no pior caso. Ou seja, para todos os pares (𝑠,𝑡) de vértices no grafo, o comprimento do caminho retornado pelo WormHole é no máximo 𝑂(loglog𝑛) maior que a distância real entre 𝑠 e 𝑡. Isto implica trivialmente que o erro aditivo médio do WormHole é, com alta probabilidade, limitado pela mesma quantidade.

\

\

4.4 Complexidade de Consulta

Recordemos o modelo de consulta de nós neste artigo (ver §1.2): começando de um único nó, podemos fazer consultas iterativamente, onde cada consulta recupera a lista de vizinhos de um nó 𝑣 à nossa escolha. Estamos interessados na complexidade de consulta, ou seja, o número de consultas necessárias para realizar certas operações.

\ \

\ \ O primeiro resultado é o limite superior do nosso desempenho.

\ \

\ \ Esboço da Prova. Para uma dada consulta SP(𝑢, 𝑣), damos um limite superior na complexidade de consulta do BFS que começa em 𝑢, e similarmente para 𝑣; a complexidade total de consulta é a soma destas duas quantidades.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info Autores:

(1) Talya Eden, Universidade Bar-Ilan (talyaa01@gmail.com);

(2) Omri Ben-Eliezer, MIT (omrib@mit.edu);

(3) C. Seshadhri, UC Santa Cruz (sesh@ucsc.edu).

:::

:::info Este artigo está disponível no arxiv sob licença CC BY 4.0.

:::

\