Dentro da Lógica dos "Produtos" e Igualdade na Teoria dos Conjuntos
Tabela De Links
Resumo
- Agradecimentos e Introdução
2. Propriedades universais
3. Produtos na prática
4. Propriedades universais na geometria algébrica
5. O problema com o uso de igualdade de Grothendieck.
6. Mais sobre mapas "canônicos"
7. Isomorfismos canônicos em matemática mais avançada
8. Resumo e Referências
Propriedades Universais
Estou ciente de três classes razoáveis de fundamentos para a matemática: aquelas baseadas na teoria dos conjuntos, aquelas baseadas na teoria dos tipos e aquelas baseadas na teoria das categorias. Existem também vários resultados que dizem que, de modo geral, esses fundamentos são capazes de provar os mesmos teoremas. No entanto, para que uma discussão sobre igualdade ocorra, teremos que definir exatamente sobre o que estamos falando, e por isso escolherei a teoria dos conjuntos ZFC e a lógica clássica como base para nossa discussão.1
A base para esta decisão é simplesmente que se um matemático alguma vez frequentou uma aula sobre os fundamentos lógicos de sua disciplina (e muitos deles não o fizeram), então provavelmente teria sido uma aula de teoria dos conjuntos. Além disso, a literatura de matemática pura é escrita num estilo superficialmente teórico de conjuntos: somos informados que um grupo é um conjunto com alguma estrutura e axiomas, uma variedade é um conjunto com uma estrutura e axiomas diferentes, e assim por diante. Aqui a palavra "conjunto" é apenas um espaço reservado para a ideia de uma "coleção de átomos".
É óbvio que dois conjuntos que são iguais têm os mesmos elementos; isto segue do chamado princípio de substituição para igualdade, que afirma que se X e Y são quaisquer dois objetos matemáticos que são iguais, então qualquer afirmação que você possa fazer em seu sistema fundamental sobre X também é verdadeira para Y. O inverso, que dois conjuntos com os mesmos elementos são iguais, é imposto como um axioma da teoria. Isso garante que o conceito abstrato de um conjunto coincida com nosso modelo mental do que ele está representando: um conjunto não é mais nem menos do que uma coleção de coisas.
Agora gostaria de iniciar a discussão sobre propriedades que caracterizam exclusivamente um objeto matemático. Comecemos com um exemplo: o produto X × Y de dois conjuntos X e Y. Deixe-me avisar o leitor agora que nos próximos parágrafos farei uma distinção muito cuidadosa entre o conceito do produto de X e Y, e o conceito de um produto de X e Y. O produto X × Y de dois conjuntos é definido como o conjunto de pares ordenados (x, y) com x ∈ X e y ∈ Y (pode-se verificar usando os axiomas da teoria dos conjuntos que é possível criar este conjunto).
Note que aqui nos deparamos com o mesmo problema que vimos anteriormente com os números reais: existem várias maneiras distintas de definir o conceito de um par ordenado na teoria dos conjuntos. A teoria dos conjuntos é muito bem projetada para trabalhar com pares não ordenados: os conjuntos {x, y} e {y, x} têm os mesmos elementos e, portanto, são iguais, então para definir um par ordenado é necessário usar algum tipo de artifício.
A página da Wikipedia para pares ordenados [Wik04b] atualmente apresenta três construções distintas, devido a Wiener ({{{x}, ∅}, {{y}}}), Hausdorff ({{x, 1}, {y, 2}}) e Kurotowski ({{x}, {x, y}}); todas têm o ar de serem um pouco artificiais.2 Novamente, os matemáticos estão bem cientes de que esta questão não importa na prática: tudo o que precisamos saber é a propriedade definidora de pares ordenados, que é que (x1, y1) = (x2, y2) ⇐⇒ x1 = x2 e y1 = y2; isto é tudo o que precisaremos, e todas as definições satisfazem esta propriedade.
O produto X × Y é equipado com dois mapas de projeção π1 : X × Y → X e π2 : X × Y → Y. Estritamente falando, não é apenas o produto, mas o triplo (X × Y, π1, π2) que satisfaz a seguinte propriedade universal:
A propriedade universal dos produtos: Um triplo (P, π1 : P → X, π2 : P → Y) é chamado de produto de X e Y se satisfizer a seguinte propriedade: se S é qualquer conjunto, e f : S → X e g : S → Y são funções, então existe uma única função de S para P tal que sua composição com π1 é f e sua composição com π2 é g.
A propriedade universal não é uma definição do produto de dois conjuntos; pode ser pensada como infinitos fatos que um produto precisa satisfazer (um para cada escolha de conjunto S e funções f e g). Não é difícil verificar que o produto X × Y de X e Y, equipado com as projeções naturais, é um produto. Mas o inverso não é verdadeiro: normalmente existem muitos outros triplos (P, π1, π2) que satisfazem a propriedade de ser um produto sem ser o produto.
Por exemplo, se X = {37} e Y = {42}, então o produto X × Y é {(37, 42)}, mas na verdade qualquer conjunto P com um elemento, equipado com π1 : P → X enviando tudo para 37 e π2 : P → Y enviando tudo para 42, satisfaz a propriedade universal de ser um produto. Em particular, existem em geral incontáveis coisas diferentes que satisfazem a propriedade de ser um produto. No entanto, os matemáticos são extremamente bons em identificar essas coisas diferentes; elas são "as mesmas" de uma maneira que transcende o uso correto do símbolo =. Podemos fazer isso por causa do yoga de unicidade para objetos universais. Vamos passar por este yoga, que é uma peça de absurdo formal teórico-categórico, no caso dos produtos.
Digamos que P1 e P2 são ambos um produto para X e Y. Aplicando a parte de existência da propriedade universal para P2 (com suas projeções para X e Y) ao conjunto S = P1 (com suas projeções para X e Y) nos dá uma função α : P1 → P2 comutando com as projeções para X e Y. Trocando os 1s e 2s no argumento, também podemos construir uma função β : P2 → P1 comutando com as projeções. Além disso, β ◦ α é um mapa de P1 para P1 comutando com as projeções, assim como a função identidade; pela parte de unicidade da propriedade universal de P1 aplicada a P1, deduzimos que β ◦ α deve ser o mapa de identidade em P1; similarmente, α ◦ β deve ser o mapa de identidade em P2.
Portanto, α e β são bijeções comutando com os mapas de projeção. Finalmente, usando a parte de unicidade da propriedade universal para P2 aplicada a P1 nos diz que α é o único mapa de P1 para P2 que comuta com as projeções, por simetria β é o único mapa de P2 para P1 que comuta com as projeções. O resultado deste absurdo abstrato (que nunca mencionou elementos de quaisquer conjuntos, apenas objetos e morfismos) é que existem bijeções mutuamente inversas únicas entre P1 e P2 que comutam com as projeções para os fatores X e
Y. Em particular, se P é um produto de X e Y, então é unicamente isomórfico ao produto X × Y de X e Y de uma maneira compatível com as projeções. Em nosso exemplo de um elemento X = {37} e Y = {42}, se P é qualquer conjunto de um elemento, então o mapa único de P para X × Y, é claro, envia o elemento para (37, 42).
:::info Autor: KEVIN BUZZARD
:::
:::info Este artigo está disponível no arxiv sob a licença CC BY 4.0 DEED.
:::
\
Você também pode gostar
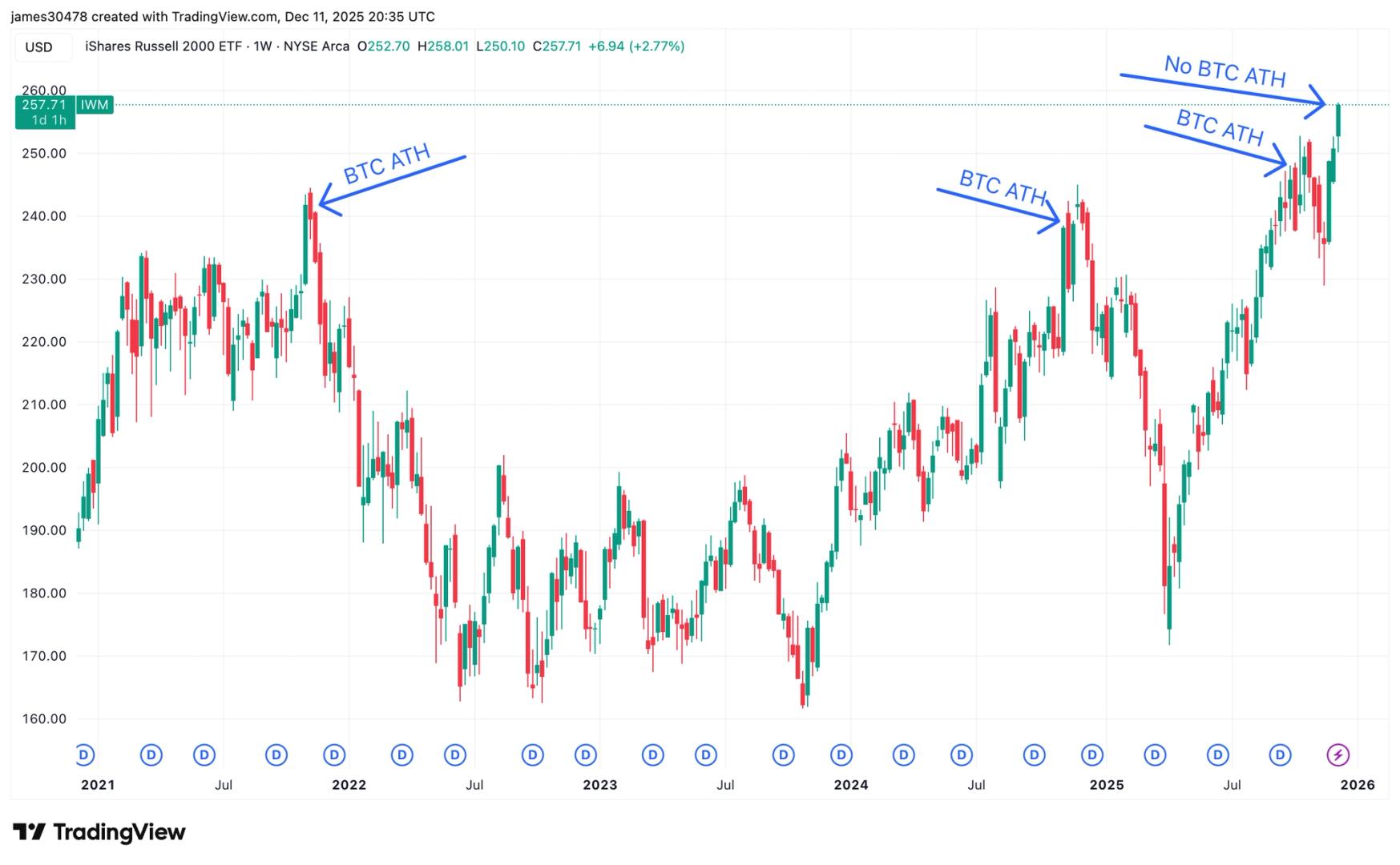
De sincronização a atraso, Bitcoin pronto para alcançar as altas das small caps
Copiar linkX (Twitter)LinkedInFacebookEmail

A profissão que protege bilhões e tem vagas sobrando no Brasil
