Руководство гика по экспериментам с машинным обучением

Таблица ссылок

Резюме и 1. Введение

1.1 Пост-хок объяснение

1.2 Проблема разногласий

1.3 Поощрение консенсуса объяснений

1. Связанные работы

2. Pear: Регуляризатор согласования пост-хок объяснений

3. Эффективность обучения консенсусу

   4.1 Метрики согласования

   4.2 Улучшение метрик консенсуса

   [4.3 Согласованность какой ценой?]()

   4.4 Являются ли объяснения все еще ценными?

   4.5 Консенсус и линейность

   4.6 Два члена функции потерь

4. Обсуждение

   5.1 Будущая работа

   5.2 Заключение, благодарности и ссылки

Приложение

A ПРИЛОЖЕНИЕ

A.1 Наборы данных

В наших экспериментах мы используем табличные наборы данных, изначально из OpenML и собранные в набор эталонных данных от команды Inria-Soda на HuggingFace [11]. Мы предоставляем некоторые детали о каждом наборе данных:

\ Bank Marketing Это набор данных бинарной классификации с шестью входными признаками и примерно сбалансированными классами. Мы обучаем на 7 933 обучающих образцах и тестируем на оставшихся 2 645 образцах.

\ California Housing Это набор данных бинарной классификации с семью входными признаками и примерно сбалансированными классами. Мы обучаем на 15 475 обучающих образцах и тестируем на оставшихся 5 159 образцах.

\ Electricity Это набор данных бинарной классификации с семью входными признаками и примерно сбалансированными классами. Мы обучаем на 28 855 обучающих образцах и тестируем на оставшихся 9 619 образцах.

A.2 Гиперпараметры

Многие из наших гиперпараметров постоянны во всех наших экспериментах. Например, все MLP обучаются с размером пакета 64 и начальной скоростью обучения 0,0005. Кроме того, все изучаемые нами MLP имеют 3 скрытых слоя по 100 нейронов каждый. Мы всегда используем оптимизатор AdamW [19]. Количество эпох варьируется от случая к случаю. Для всех трех наборов данных мы обучаем в течение 30 эпох, когда 𝜆 ∈ {0,0, 0,25}, и 50 эпох в остальных случаях. При обучении линейных моделей мы используем 10 эпох и начальную скорость обучения 0,1.

A.3 Метрики разногласий

Здесь мы определяем каждую из шести метрик согласования, используемых в нашей работе.

\ Первые четыре метрики зависят от топ-𝑘 наиболее важных признаков в каждом объяснении. Пусть 𝑡𝑜𝑝_𝑓 𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘) представляет топ-𝑘 наиболее важных признаков в объяснении 𝐸, пусть 𝑟𝑎𝑛𝑘 (𝐸, 𝑠) будет рангом важности признака 𝑠 в объяснении 𝐸, и пусть 𝑠𝑖𝑔𝑛(𝐸, 𝑠) будет знаком (положительным, отрицательным или нулевым) оценки важности признака 𝑠 в объяснении 𝐸.

\

\ Следующие две метрики согласования зависят от всех признаков в каждом объяснении, а не только от топ-𝑘. Пусть 𝑅 будет функцией, которая вычисляет ранжирование признаков в объяснении по важности.

\

\ (Примечание: Krishna и др. [15] указывают в своей статье, что 𝐹 должен быть набором признаков, указанных конечным пользователем, но в наших экспериментах мы используем все признаки с этой метрикой).

A.4 Результаты эксперимента с бесполезными признаками

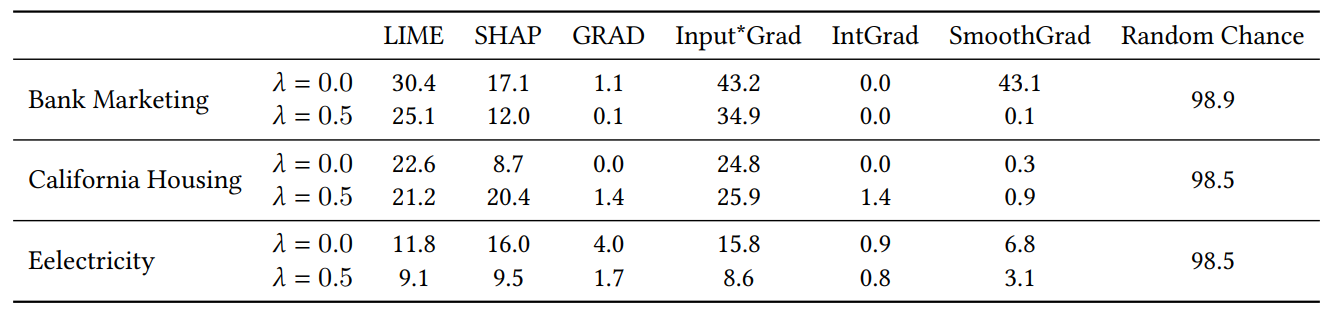
Когда мы добавляем случайные признаки для эксперимента в разделе 4.4, мы удваиваем количество признаков. Мы делаем это, чтобы проверить, ухудшает ли наша функция потерь консенсуса качество объяснения, помещая нерелевантные признаки в топ-𝐾 чаще, чем модели, обученные естественным образом. В Таблице 1 мы сообщаем процент случаев, когда каждый объяснитель включал один из случайных признаков в топ-5 наиболее важных признаков. Мы наблюдаем, что в целом мы не видим систематического увеличения этих процентов между 𝜆 = 0,0 (базовый MLP без нашей функции потерь консенсуса) и 𝜆 = 0,5 (MLP, обученный с нашей функцией потерь консенсуса)

\

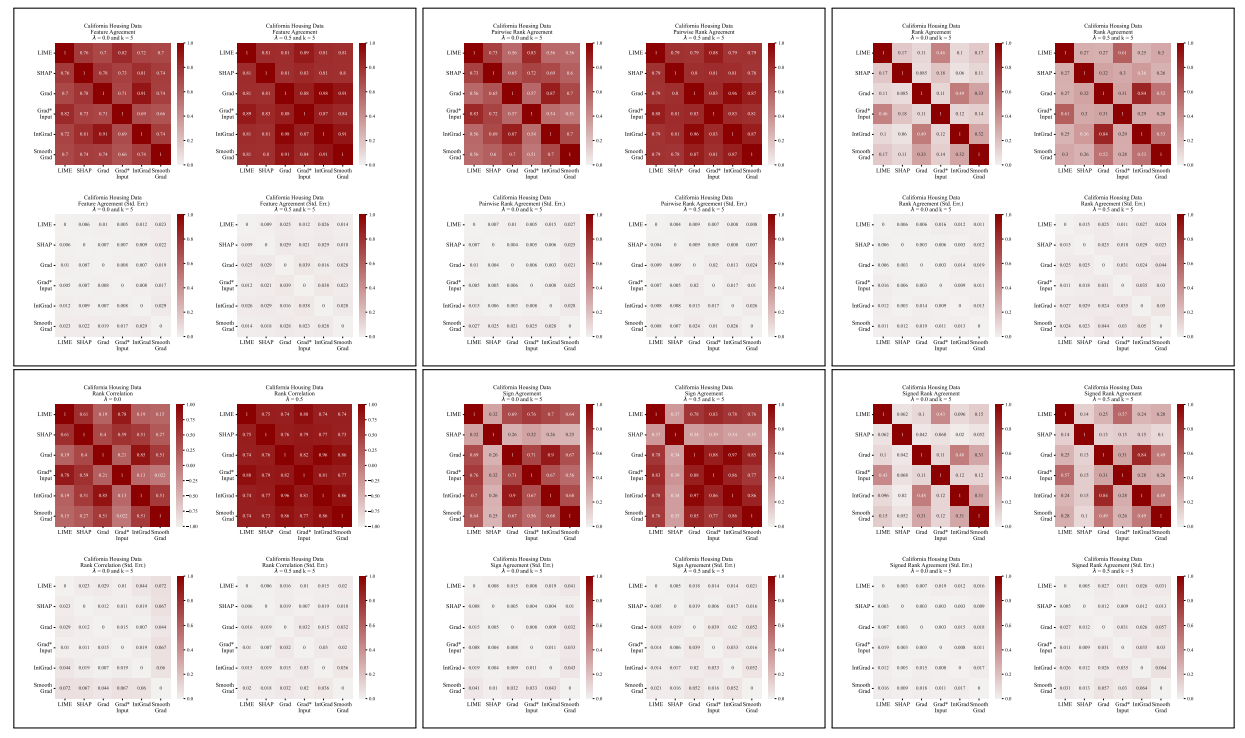
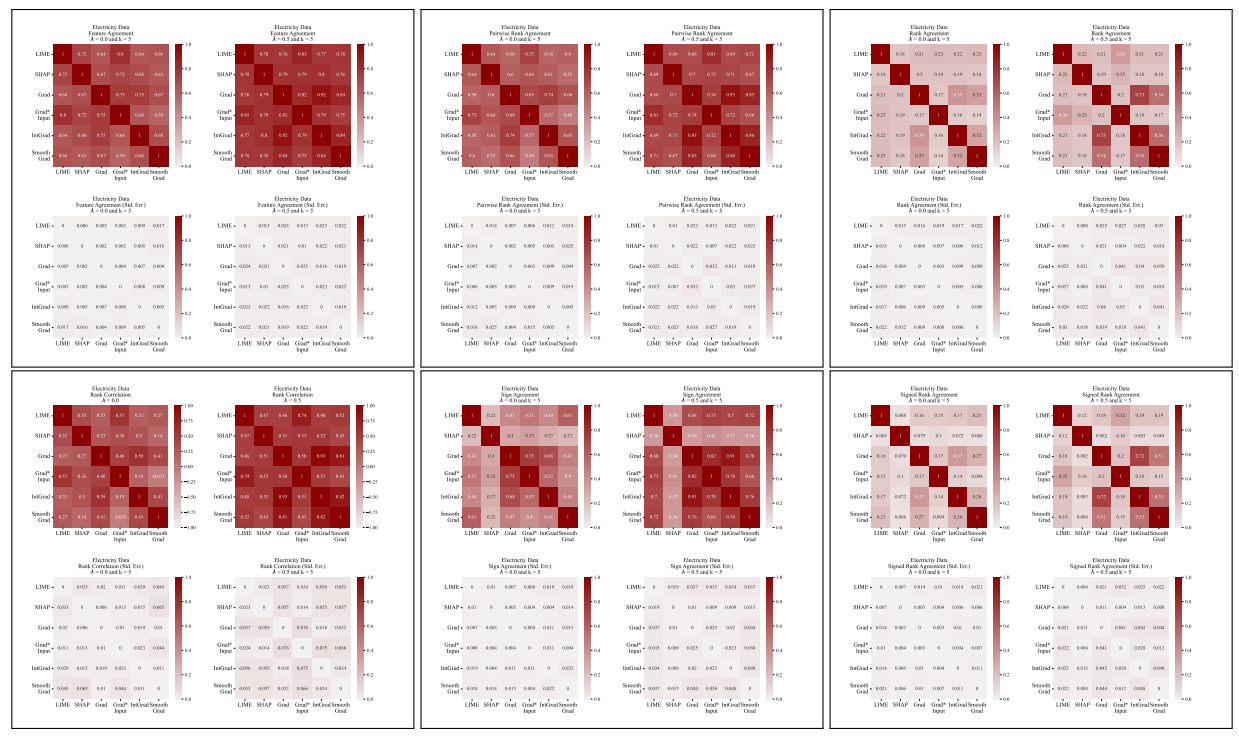
A.5 Дополнительные матрицы разногласий

\

\

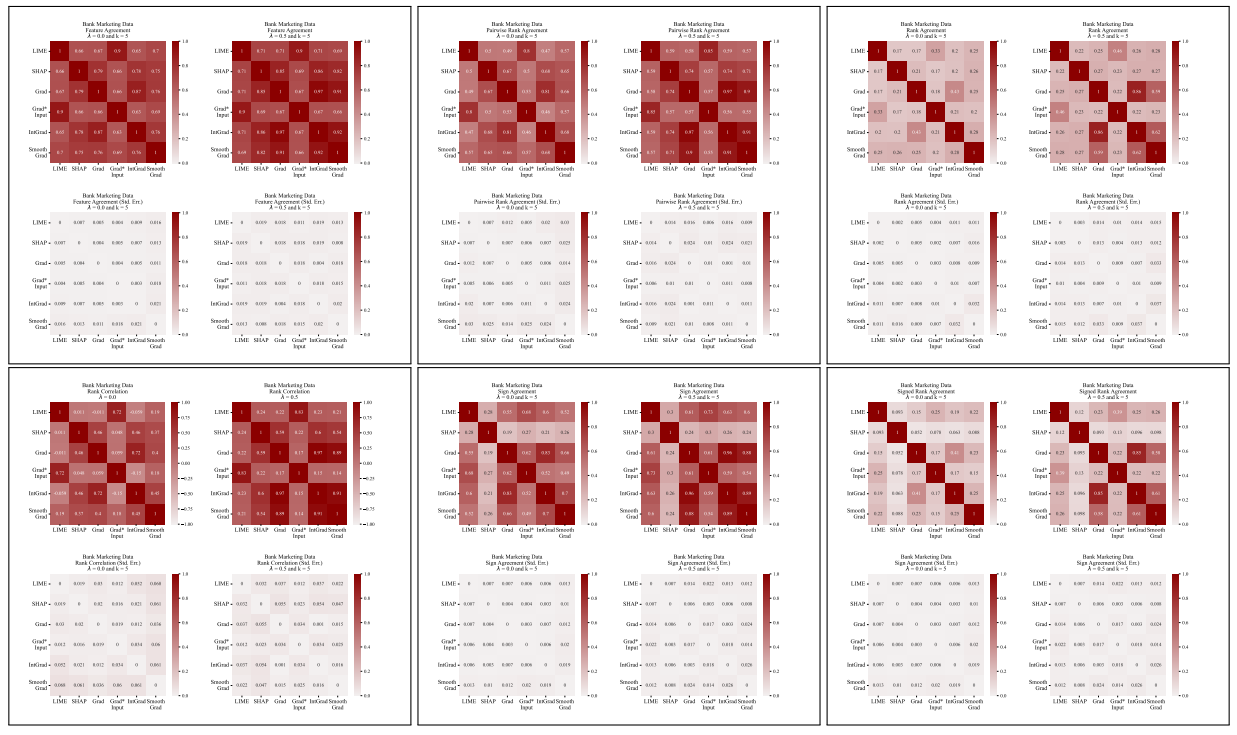
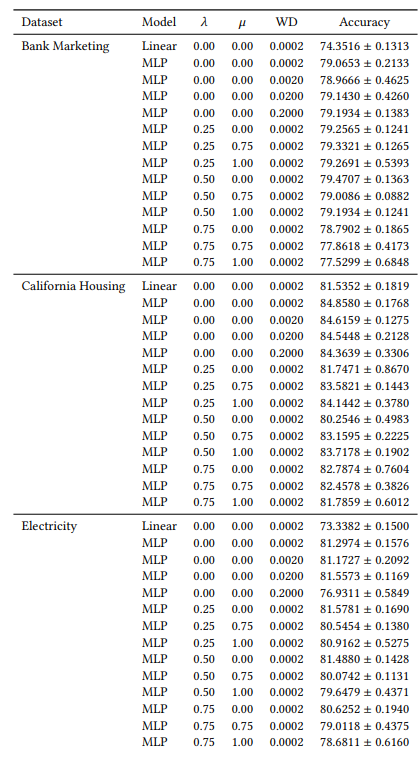
A.6 Расширенные результаты

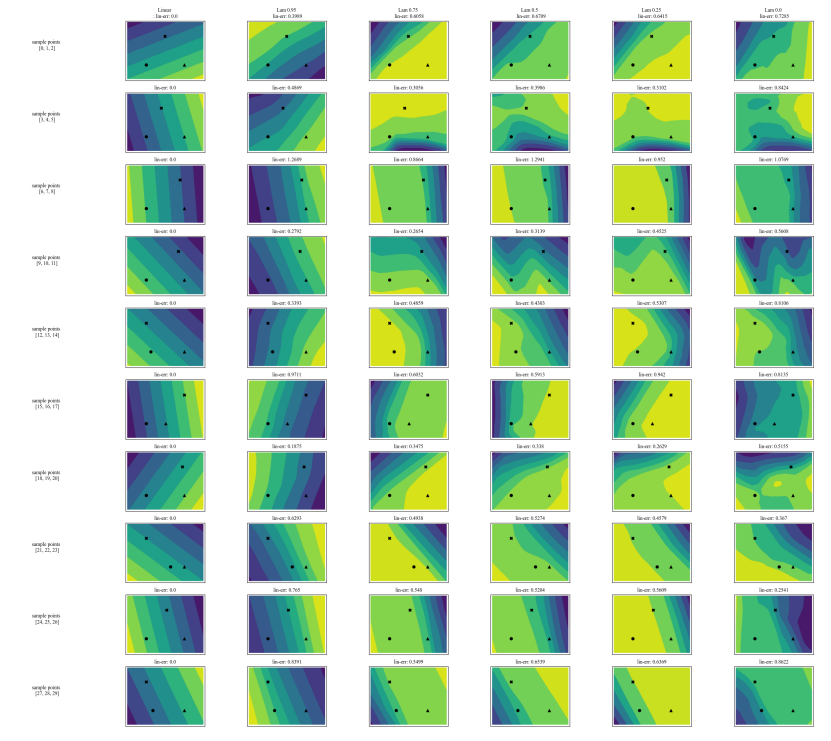
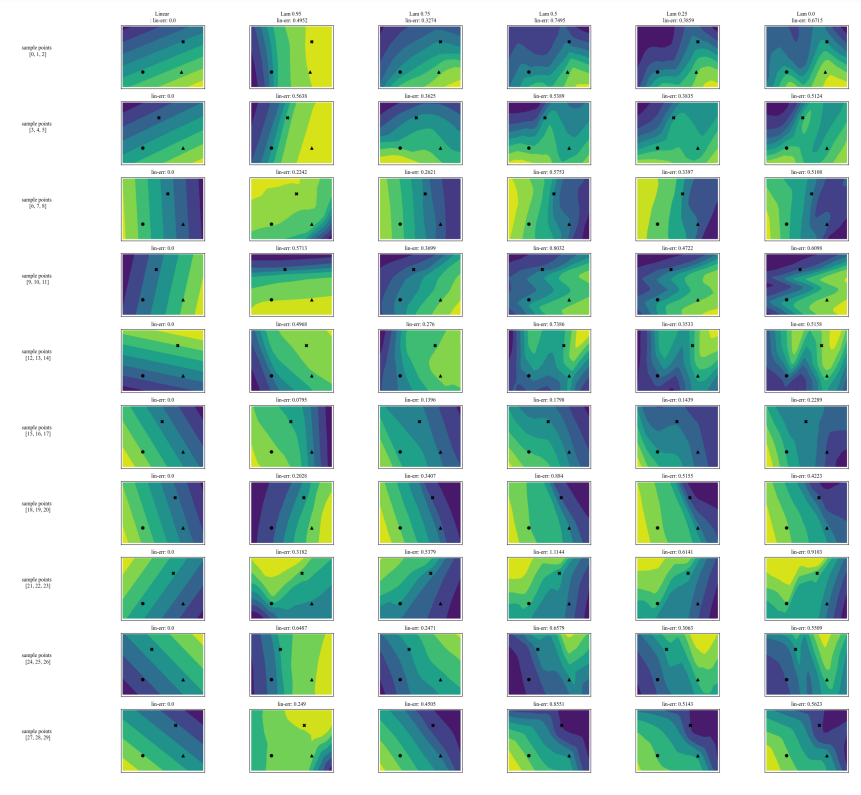
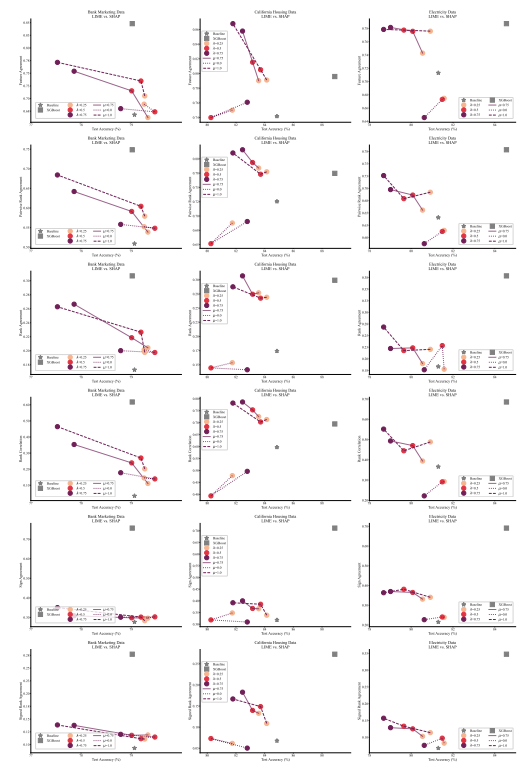
A.7 Дополнительные графики

\

\

\

\

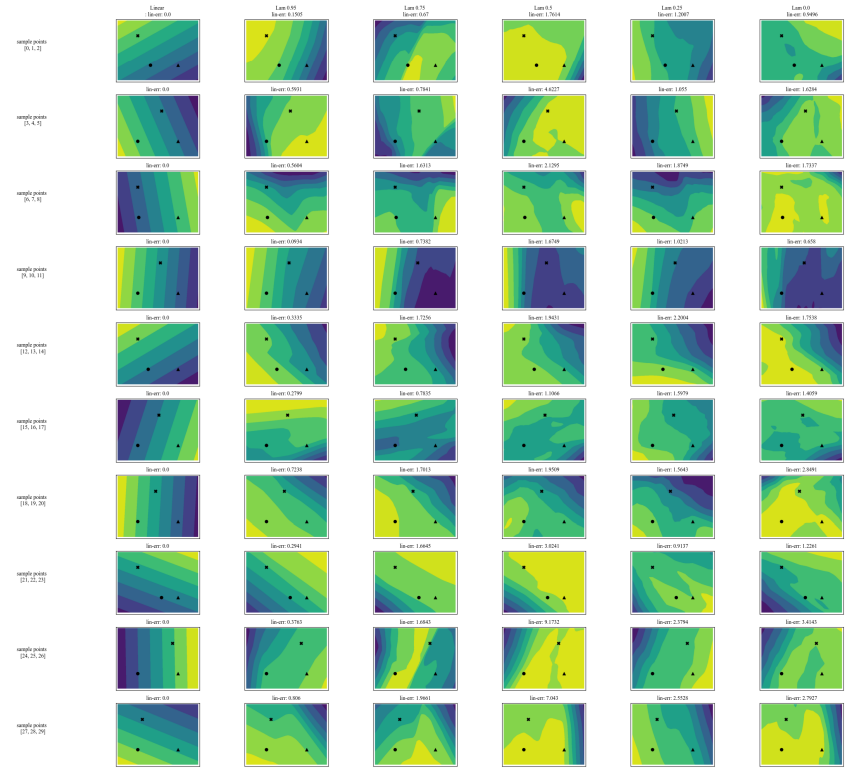
:::info Авторы:

(1) Ави Шварцшильд, Университет Мэриленда, Колледж-Парк, Мэриленд, США и работа выполнена во время работы в Arthur (avi1umd.edu);

(2) Макс Цембалест, Arthur, Нью-Йорк, Нью-Йорк, США;

(3) Картик Рао, Arthur, Нью-Йорк, Нью-Йорк, США;

(4) Киган Хайнс, Arthur, Нью-Йорк, Нью-Йорк, США;

(5) Джон Дикерсон†, Arthur, Нью-Йорк, Нью-Йорк, США (john@arthur.ai).

:::

:::info Эта статья доступна на arxiv под лицензией CC BY 4.0 DEED.

:::

\