Как WormHole ускоряет поиск пути в графах с миллиардами рёбер

Таблица ссылок

Резюме и 1. Введение

1.1 Наш вклад

1.2 Настройка

1.3 Алгоритм

1. Связанные работы

2. Алгоритм

   3.1 Фаза структурной декомпозиции

   3.2 Фаза маршрутизации

   3.3 Варианты WormHole

3. Теоретический анализ

   4.1 Предварительные сведения

   4.2 Сублинейность внутреннего кольца

   4.3 Ошибка аппроксимации

   4.4 Сложность запроса

4. Экспериментальные результаты

   5.1 WormHole𝐸, WormHole𝐻 и BiBFS

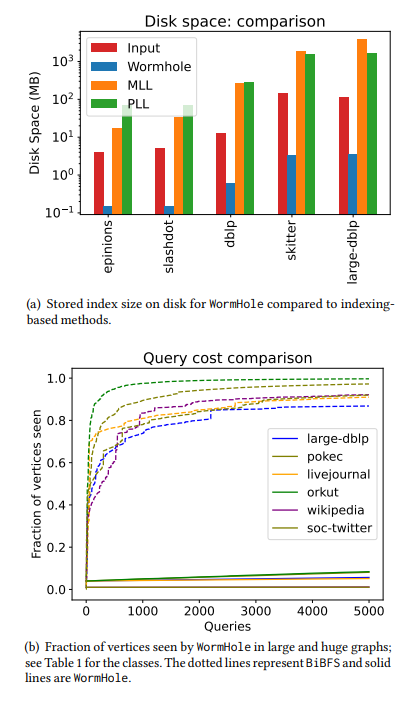
   5.2 Сравнение с методами на основе индексации

   5.3 WormHole как примитив: WormHole𝑀

Ссылки

1.1 Наш вклад

Мы разрабатываем новый алгоритм, WormHole, который создает структуру данных, позволяющую отвечать на множественные запросы о кратчайших путях, используя типичную структуру многих социальных и информационных сетей. WormHole прост, легко реализуем и теоретически обоснован. Мы предоставляем несколько его вариантов, каждый из которых подходит для разных условий, демонстрируя отличные эмпирические результаты на различных наборах сетевых данных. Ниже приведены некоторые из его ключевых особенностей:

\ • Компромисс между производительностью и точностью. Насколько нам известно, наш алгоритм является первым приближенным сублинейным алгоритмом кратчайших путей в больших сетях. Тот факт, что мы допускаем небольшую аддитивную ошибку, приводит к компромиссу между временем/пространством предварительной обработки и временем на запрос, и позволяет нам прийти

\

\ к решению с эффективной предварительной обработкой и быстрым временем на запрос. Примечательно, что наш самый точный (но самый медленный) вариант, WormHole𝐸, имеет почти идеальную точность: более 90% запросов получают ответ без аддитивной ошибки, и во всех сетях более 99% запросов получают ответ с аддитивной ошибкой не более 2. Подробнее см. в Таблице 3.

\ • Чрезвычайно быстрое время настройки. Наше самое длительное время построения индекса составило всего две минуты даже для графов с миллиардами ребер. Для контекста, PLL и MLL превысили лимит времени на половине сетей, которые мы тестировали, а для графов среднего размера, где PLL и MLL завершили свои запуски, построение индекса WormHole было в 100 раз быстрее. А именно, WormHole завершился за секунды, в то время как PLL занял часы. См. Таблицу 4 и Таблицу 5. Это быстрое время настройки достигается благодаря использованию индекса сублинейного размера. Для самых больших сетей, которые мы рассматривали, достаточно взять индекс примерно 1% узлов, чтобы получить малую среднюю аддитивную ошибку – см. Таблицу 1. Для меньших сетей это может быть до 6%.

\ • Быстрое время запроса. По сравнению с BiBFS, ванильная версия WormHole𝐸 (без каких-либо оптимизаций на основе индексов) в 2 раза быстрее для почти всех графов и более чем в 4 раза быстрее на трех самых больших графах, которые мы тестировали. Простой вариант WormHole𝐻 достигает улучшения на порядок за счет некоторой потери точности: стабильно в 20 раз быстрее почти на всех графах и более чем в 180 раз для самого большого графа, который у нас есть. Полное сравнение см. в Таблице 3. Методы на основе индексации обычно отвечают на запросы за микросекунды; оба вышеупомянутых варианта все еще находятся в режиме миллисекунд.

\ • Комбинирование WormHole и современных методов. WormHole работает, сохраняя небольшое подмножество вершин, на которых мы вычисляем точные кратчайшие пути. Для произвольных запросов мы направляем наш путь через это подмножество, которое мы называем ядром. Мы используем это понимание, чтобы предоставить третий вариант, WormHole𝑀, реализуя современный метод для кратчайших путей, MLL, на ядре. Это достигает времени запроса, сопоставимого с MLL (с той же гарантией точности, что и WormHole𝐻), при доле стоимости настройки, и работает для массивных графов, где MLL не завершается. Мы исследуем этот комбинированный подход в §5.3 и предоставляем статистику в Таблице 6.

\ • Сублинейная сложность запроса. Сложность запроса относится к количеству вершин, запрашиваемых алгоритмом. В модели с ограниченным доступом к запросам, где запрос узла раскрывает его список соседей (см. §1.2), сложность запроса нашего алгоритма очень хорошо масштабируется с количеством запросов расстояния/кратчайшего пути. Чтобы ответить на 5000 приближенных запросов о кратчайшем пути, наш алгоритм наблюдает только от 1% до 20% узлов для большинства сетей. Для сравнения, BiBFS видит более 90% графа, чтобы ответить на несколько сотен запросов о кратчайшем пути. См. Рисунок 2 и Рисунок 5 для сравнения.

\ • Доказуемые гарантии по ошибке и производительности. В §4 мы доказываем набор теоретических результатов, дополняющих и объясняющих эмпирическую производительность. Результаты, неформально изложенные ниже, доказаны для модели случайных графов Чунг-Лу со степенным распределением степеней [15–17].

\ Теорема 1.1 (Неформально). В случайном графе Чунг-Лу 𝐺 со степенным показателем 𝛽 ∈ (2,3) на 𝑛 вершинах, WormHole имеет следующие гарантии с высокой вероятностью:

\

\

:::info Авторы:

(1) Talya Eden, Bar-Ilan University (talyaa01@gmail.com);

(2) Omri Ben-Eliezer, MIT (omrib@mit.edu);

(3) C. Seshadhri, UC Santa Cruz (sesh@ucsc.edu).

:::

:::info Эта статья доступна на arxiv под лицензией CC BY 4.0.

:::

\