Як WormHole прискорює пошук шляхів у графах з мільярдами ребер

Таблиця посилань

Анотація та 1. Вступ

1.1 Наш внесок

1.2 Налаштування

1.3 Алгоритм

1. Пов'язані роботи

2. Алгоритм

   3.1 Фаза структурної декомпозиції

   3.2 Фаза маршрутизації

   3.3 Варіанти WormHole

3. Теоретичний аналіз

   4.1 Передумови

   4.2 Сублінійність внутрішнього кільця

   4.3 Похибка апроксимації

   4.4 Складність запиту

4. Експериментальні результати

   5.1 WormHole𝐸, WormHole𝐻 та BiBFS

   5.2 Порівняння з методами на основі індексації

   5.3 WormHole як примітив: WormHole𝑀

Посилання

1.1 Наш внесок

Ми розробили новий алгоритм, WormHole, який створює структуру даних, що дозволяє відповідати на численні запити щодо найкоротших шляхів, використовуючи типову структуру багатьох соціальних та інформаційних мереж. WormHole простий, легкий у реалізації та теоретично обґрунтований. Ми надаємо кілька його варіантів, кожен з яких підходить для різних умов, демонструючи відмінні емпіричні результати на різноманітних наборах мережевих даних. Нижче наведені деякі з його ключових особливостей:

\ • Компроміс між продуктивністю та точністю. Наскільки нам відомо, наш алгоритм є першим приблизним сублінійним алгоритмом найкоротших шляхів у великих мережах. Той факт, що ми допускаємо невелику адитивну похибку, призводить до компромісу між часом/простором попередньої обробки та часом на запит, і дозволяє нам прийти

\

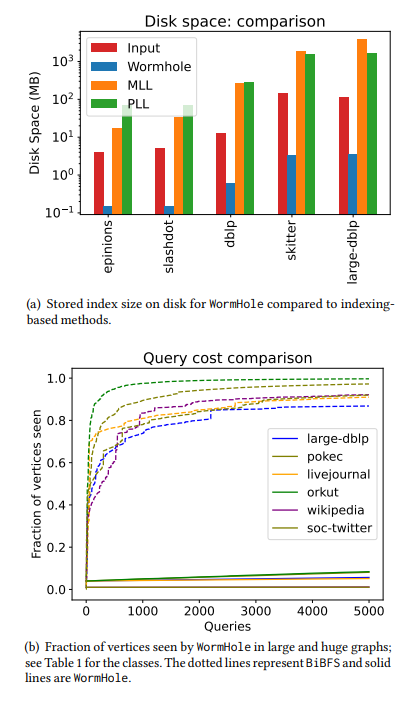
\ до рішення з ефективною попередньою обробкою та швидким часом на запит. Зокрема, наш найточніший (але найповільніший) варіант, WormHole𝐸, має майже ідеальну точність: більше 90% запитів отримують відповідь без адитивної похибки, а в усіх мережах більше 99% запитів отримують відповідь з адитивною похибкою не більше 2. Див. Таблицю 3 для більш детальної інформації.

\ • Надзвичайно швидкий час налаштування. Наш найдовший час побудови індексу становив лише дві хвилини навіть для графів з мільярдами ребер. Для контексту, PLL та MLL вичерпали час очікування на половині мереж, які ми тестували, а для графів середнього розміру, де PLL та MLL завершили свої запуски, побудова індексу WormHole була в 100 разів швидшою. А саме, WormHole завершився за секунди, тоді як PLL займав години. Див. Таблицю 4 та Таблицю 5. Цей швидкий час налаштування досягається завдяки використанню індексу сублінійного розміру. Для найбільших мереж, які ми розглядали, достатньо взяти індекс приблизно 1% вузлів, щоб отримати малу середню адитивну похибку – див. Таблицю 1. Для менших мереж це може бути до 6%.

\ • Швидкий час запиту. У порівнянні з BiBFS, ванільна версія WormHole𝐸 (без будь-яких оптимізацій на основі індексації) у 2 рази швидша для майже всіх графів і більш ніж у 4 рази швидша на трьох найбільших графах, які ми тестували. Простий варіант WormHole𝐻 досягає покращення на порядок за рахунок деякої втрати точності: стабільно у 20 разів швидше майже на всіх графах і більш ніж у 180 разів для найбільшого графа, який у нас є. Див. Таблицю 3 для повного порівняння. Методи на основі індексації зазвичай відповідають на запити за мікросекунди; обидва згадані варіанти все ще знаходяться в режимі мілісекунд.

\ • Поєднання WormHole та сучасних технологій. WormHole працює, зберігаючи невелику підмножину вершин, на яких ми обчислюємо точні найкоротші шляхи. Для довільних запитів ми прокладаємо наш шлях через цю підмножину, яку ми називаємо ядром. Ми використовуємо це розуміння, щоб надати третій варіант, WormHole𝑀, реалізуючи найсучасніший метод для найкоротших шляхів, MLL, на ядрі. Це досягає часу запиту, порівнянного з MLL (з тією ж гарантією точності, що й WormHole𝐻) за частку вартості налаштування, і працює для масивних графів, де MLL не завершується. Ми досліджуємо цей комбінований підхід у §5.3 і надаємо статистику в Таблиці 6.

\ • Сублінійна складність запиту. Складність запиту відноситься до кількості вершин, запитаних алгоритмом. У моделі обмеженого доступу до запитів, де запит до вузла розкриває його список сусідів (див. §1.2), складність запиту нашого алгоритму дуже добре масштабується з кількістю зроблених запитів щодо відстані / найкоротшого шляху. Щоб відповісти на 5000 приблизних запитів найкоротшого шляху, наш алгоритм спостерігає лише від 1% до 20% вузлів для більшості мереж. Для порівняння, BiBFS бачить більше 90% графа, щоб відповісти на кілька сотень запитів найкоротшого шляху. Див. Рисунок 2 та Рисунок 5 для порівняння.

\ • Доведені гарантії щодо похибки та продуктивності. У §4 ми доводимо набір теоретичних результатів, що доповнюють та пояснюють емпіричну продуктивність. Результати, неформально викладені нижче, доведені для моделі випадкових графів Чунг-Лу з розподілом ступенів за степеневим законом [15–17].

\ Теорема 1.1 (Неформально). У випадковому графі Чунг-Лу 𝐺 з показником степеневого закону 𝛽 ∈ (2,3) на 𝑛 вершинах, WormHole має наступні гарантії з високою ймовірністю:

\

\

:::info Автори:

(1) Талья Еден, Університет Бар-Ілан (talyaa01@gmail.com);

(2) Омрі Бен-Еліезер, MIT (omrib@mit.edu);

(3) К. Сешадрі, Університет Каліфорнії, Санта-Крус (sesh@ucsc.edu).

:::

:::info Ця стаття доступна на arxiv за ліцензією CC BY 4.0.

:::

\