Покращення глибокого навчання за допомогою геометрії Лоренца: результати експериментів LHIER

Таблиця посилань

Анотація та 1. Вступ

1. Пов'язані роботи

2. Методологія

   3.1 Передумови

   3.2 Ріманова оптимізація

   3.3 До ефективних архітектурних компонентів

3. Експерименти

   4.1 Проблема ієрархічного метричного навчання

   4.2 Стандартна проблема класифікації

4. Висновок та посилання

4 Експерименти

4.1 Проблема ієрархічного метричного навчання

\ У наступному експерименті ми розширюємо HIER до моделі Лоренца (LHIER) і порівнюємо з результатами, наданими в [20]. Метою цього є доведення ефективності нашого оптимізатора Lorentzian AdamW, загальної схеми оптимізації, навчання кривизни та масштабування максимальної відстані.

\ Експериментальна установка Ми дотримуємося експериментальної установки в Kim et al. [20] і спираємося на чотири основні набори даних: CUB-200-2011 (CUB)[42], Cars-196 (Cars)[22], Stanford Online Product (SOP)[34] та In-shop Clothes Retrieval (InShop)[24]. Продуктивність вимірюється за допомогою Recall@k, що є часткою запитів з одним або більше релевантними зразками серед їх k-найближчих сусідів. Крім того, всі основи моделей попередньо навчені на Imagenet для забезпечення справедливих порівнянь з попередньою роботою.

\

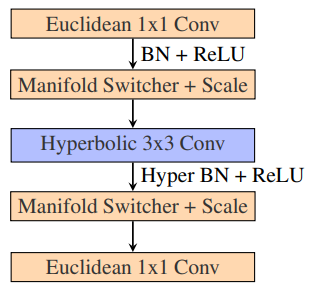
\ Перехід до простору Лоренца Ми адаптуємо HIER до гіперболоїда, використовуючи три основні зміни. Спочатку ми замінюємо евклідовий лінійний шар на лоренцівський лінійний шар у шиї моделі та впроваджуємо нашу операцію масштабування максимальної відстані після цього. Потім ми встановлюємо ієрархічні проксі як параметри гіперболічного навчання та оптимізуємо їх безпосередньо на многовиді, використовуючи наш Lorentzian AdamW. Нарешті, ми змінюємо відстань Пуанкаре на відстань Лоренца для втрати LHIER і встановлюємо ієрархічні проксі для попереднього масштабування. Ми також продовжуємо використовувати точність fp16, що показує, що наша модель більш стійка до проблем стабільності та неточності.

\ Результати Як показано в таблиці 1, наша модель HIER+ покращує продуктивність майже у всіх сценаріях. Однак відсоткова зміна варіюється залежно від набору даних та використовуваної моделі. Хоча ми досягаємо найкращих результатів у випадку моделей Resnet, ми особливо гірші для моделі DeiT, особливо при вищій розмірності, де наш метод перевершується у більшості наборів даних HIER. Це може бути проблемою відсутності налаштування гіперпараметрів, особливо у випадку масштабування tanh; фактор s, який контролює щільність виходів. Kim et al. [20] контролюють це за допомогою обрізання норми з різною інтенсивністю, подібний підхід можна було б прийняти для вивчення найкращих факторів масштабування з урахуванням експериментальних налаштувань.

4.2 Стандартна проблема класифікації

Експериментальна установка Ми дотримуємося експериментальної установки Bdeir et al. [1] і спираємося на три основні набори даних: CIFAR10, CIFAR100, Mini-Imagenet. Ми також розширюємо експерименти, включаючи Resnet50, однак через збільшення витрат пам'яті ми можемо порівнювати лише з базовим евклідовим аналогом та гібридними моделями. Для моделей Resnet-18 ми не використовуємо наші блоки ядра Лоренца, а натомість відтворюємо гібридний кодер, подібний до Bdeir et al. [1]. Для всіх моделей ми використовуємо ефективний згортковий шар, всі гіперболічні вектори масштабуються за допомогою нашого перемасштабування максимальної відстані з s = 2. Крім того, навчання кривизни виконується як для нашого Resnet-18, так і для Resnet-50 за допомогою ріманівського SGD з нашою фіксованою схемою. Многовиди кодера та декодера розділені, кожен здатний вивчати власну кривизну для кращої гнучкості.

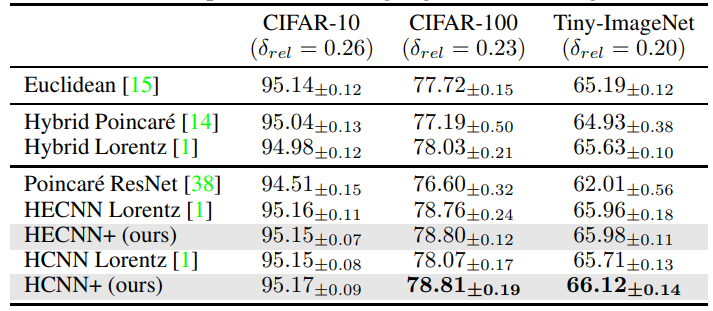
\ Результати Для тестів Resnet-18 ми бачимо в таблиці 2, що нові архітектури працюють краще у всіх сценаріях. Найменша продуктивність спостерігалася в основному між гібридними моделями, це може бути загалом тому, що гіперболічне зміщення, яке відіграють додаткові гіперболічні компоненти, не так помітне, як у повністю гіперболічній моделі. Це може призвести до того, що модель менше виграє від запропонованих змін. Ми можемо перевірити це через більший розрив у продуктивності між повністю гіперболічними моделями, де наша запропонована модель бачить підвищення точності на 74% і навіть відповідає гібридним кодерам у цьому сценарії. Для вивчення цього ми розглянули нову кривизну, вивчену кодером, і виявили, що вона має тенденцію до приблизно -0,6, що призводить до більш плоского многовиду.

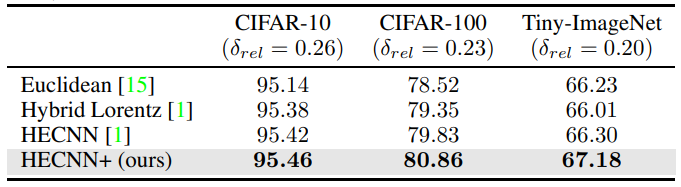
\ Що стосується тестів Resnet-50, ми бачимо в таблиці 3, що HECNN+ тепер здатний значно перевершити евклідову модель у всіх наборах даних. Навіть у випадку Tiny-Imagenet, де точність інших моделей починає руйнуватися. Це, ймовірно, пов'язано з більш плавною інтеграцією гіперболічних елементів та широким масштабуванням для допомоги у роботі з вкладеннями вищої розмірності.

\

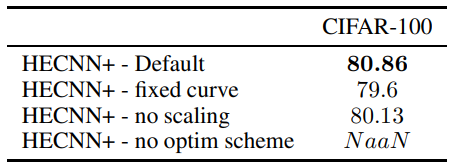
\ Абляція Ми тестуємо вплив окремих компонентів моделі в таблиці 5. Кожна наступна модель включає архітектуру за замовчуванням, представлену в експериментальній установці, за винятком згаданого компонента. Як ми бачимо, найкращі результати досягаються, коли включені всі архітектурні компоненти. У випадку спроби вивчити кривизну без запропонованої схеми оптимізатора модель повністю руйнується через надмірні числові неточності. Ще однією перевагою, яку ми знаходимо від вивчення кривизни, є швидша збіжність. Модель здатна досягти збіжності за 130 епох проти 200 епох, необхідних для моделі зі статичною кривою.

\

\

\

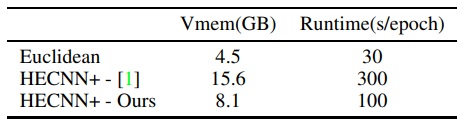
\ Потім ми вивчаємо ефективність нашої ефективної згортки в таблиці 4. Ми бачимо зменшення використання пам'яті на ∼ 48% та зменшення часу виконання на ∼ 66%. Ми приписуємо це покращення ефективним операціям згортки з закритим кодом, які ми тепер можемо використовувати. Однак все ще є багато місця для вдосконалення порівняно з евклідовою моделлю. Ми визначаємо операцію batchnorm як нове вузьке місце пам'яті та часу виконання, що становить близько 60% часу виконання та близько 30% пам'яті. Факторизація багатьох паралельних транспортів та відображень дотичних, необхідних для цієї операції, буде наступним кроком у пом'якшенні цієї проблеми.

\

\

5 Висновок

У нашій роботі ми представляємо багато нових компонентів та схем для використання гіперболічного глибокого навчання в гіперболічному зорі. Ми представляємо нову схему оптимізатора, яка дозволяє вивчати кривизну, масштабування tanh для запобігання проблемам числової точності, ріманівський оптимізатор Adam та ефективні формулювання існуючих операцій згортки. Ми тестуємо ці компоненти у двох різних проблемних сценаріях, ієрархічному метричному навчанні та класифікації, і доводимо потенціал цих нових компонентів навіть в умовах float16, які сумнозвісно нестабільні для гіперболічних моделей.

\ Однак все ще є багато прогресу, який потрібно зробити. Операції масштабування забезпечують загальний метод утримання вкладень у межах репрезентативного радіусу, але їх також можна використовувати для обрізання норми. Необхідно провести дослідження впливу обмеження вкладень для гіперболічних моделей, оскільки це вже показало свою користь [14, 20]. Крім того, більшу ефективність все ще можна отримати від гіперболічних моделей через подальшу оптимізацію шарів пакетної нормалізації. Нарешті, все ще існує проблема гіперболічного шару прямого поширення при переході від вищої до нижчої розмірності. Ми зараз зіставляємо норми для забезпечення операції обертання, але ми заохочуємо пошук альтернативних підходів, які краще відповідають математиці многовиду.

Посилання

[1] A. Bdeir, K. Schwethelm, and N. Landwehr. Fully hyperbolic convolutional neural networks for computer vision, 2024.

\ [2] M. Caron, H. Touvron, I. Misra, H. Jégou, J. Mairal, P. Bojanowski, and A. Joulin.