极客的机器学习实验指南
链接表
摘要和1. 引言
1.1 事后解释
1.2 分歧问题
1.3 鼓励解释共识
-
相关工作
-
Pear: 事后解释器一致性正则化器
-
共识训练的有效性
4.1 一致性指标
4.2 改进共识指标
[4.3 一致性的代价是什么?]()
4.4 解释是否仍然有价值?
4.5 共识和线性
4.6 两个损失项
-
讨论
5.1 未来工作
5.2 结论、致谢和参考文献
附录
A 附录
A.1 数据集
在我们的实验中,我们使用了最初来自OpenML的表格数据集,这些数据集由Inria-Soda团队编译成一组基准数据集并发布在HuggingFace上[11]。我们提供每个数据集的一些详细信息:
\ 银行营销 这是一个二元分类数据集,具有六个输入特征,类别大致平衡。我们在7,933个训练样本上进行训练,并在剩余的2,645个样本上进行测试。
\ 加州房价 这是一个二元分类数据集,具有七个输入特征,类别大致平衡。我们在15,475个训练样本上进行训练,并在剩余的5,159个样本上进行测试。
\ 电力 这是一个二元分类数据集,具有七个输入特征,类别大致平衡。我们在28,855个训练样本上进行训练,并在剩余的9,619个样本上进行测试。
A.2 超参数
我们的许多超参数在所有实验中都是恒定的。例如,所有MLP都使用64的批量大小和0.0005的初始学习率进行训练。此外,我们研究的所有MLP都有3个隐藏层,每层100个神经元。我们始终使用AdamW优化器[19]。训练轮数因情况而异。对于所有三个数据集,当𝜆∈{0.0, 0.25}时,我们训练30轮,否则训练50轮。在训练线性模型时,我们使用10轮训练和0.1的初始学习率。
A.3 分歧指标
我们在此定义我们工作中使用的六个一致性指标。
\ 前四个指标取决于每个解释中最重要的前k个特征。让𝑡𝑜𝑝_𝑓𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘)表示解释𝐸中最重要的前k个特征,让𝑟𝑎𝑛𝑘(𝐸, 𝑠)表示特征𝑠在解释𝐸中的重要性排名,让𝑠𝑖𝑔𝑛(𝐸, 𝑠)表示特征𝑠在解释𝐸中重要性分数的符号(正、负或零)。
\ 
\ 接下来的两个一致性指标取决于每个解释中的所有特征,而不仅仅是前k个。让𝑅是一个函数,用于计算解释中按重要性排序的特征排名。
\ 
\ (注:Krishna等人[15]在他们的论文中指出,𝐹应该是由最终用户指定的一组特征,但在我们的实验中,我们使用此指标时包含所有特征)。
A.4 无用特征实验结果
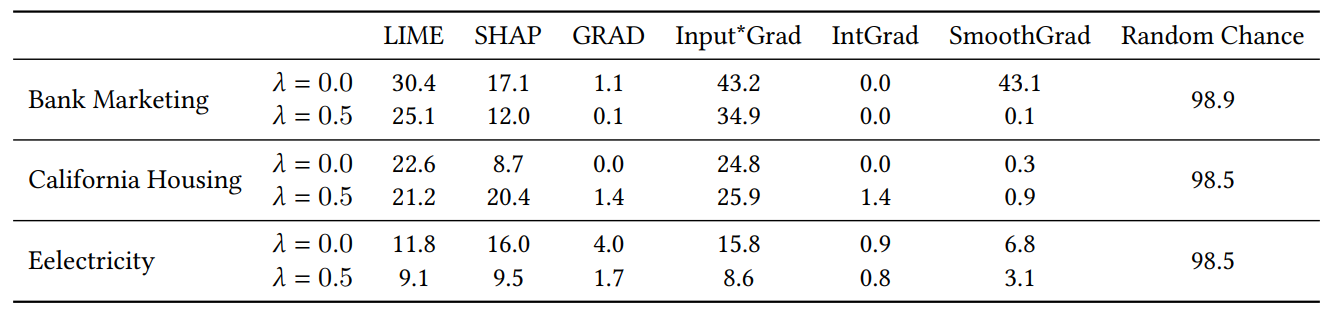
当我们为第4.4节的实验添加随机特征时,我们将特征数量翻倍。我们这样做是为了检查我们的共识损失是否会通过比自然训练的模型更频繁地将不相关特征放在前K位而损害解释质量。在表1中,我们报告了每个解释器将随机特征之一包含在前5个最重要特征中的百分比。我们观察到,总体而言,我们没有看到在𝜆=0.0(没有我们的共识损失的基准MLP)和𝜆=0.5(使用我们的共识损失训练的MLP)之间这些百分比的系统性增加
\ 
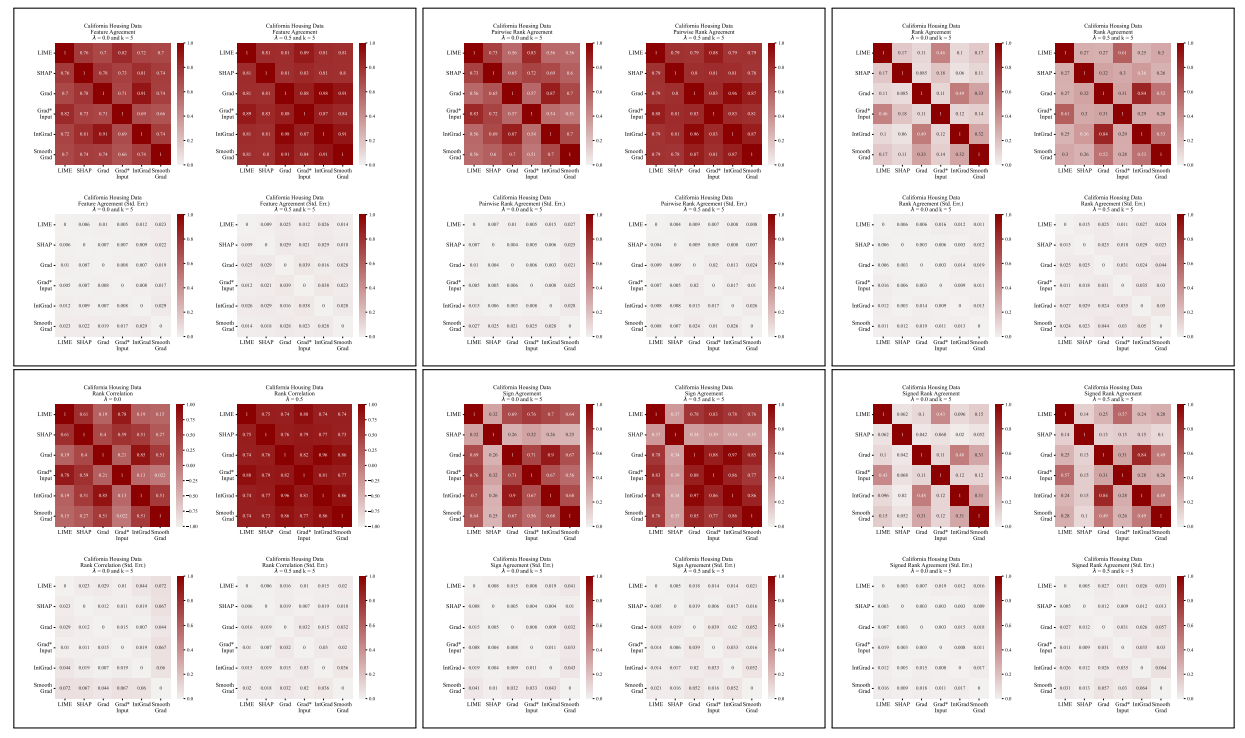
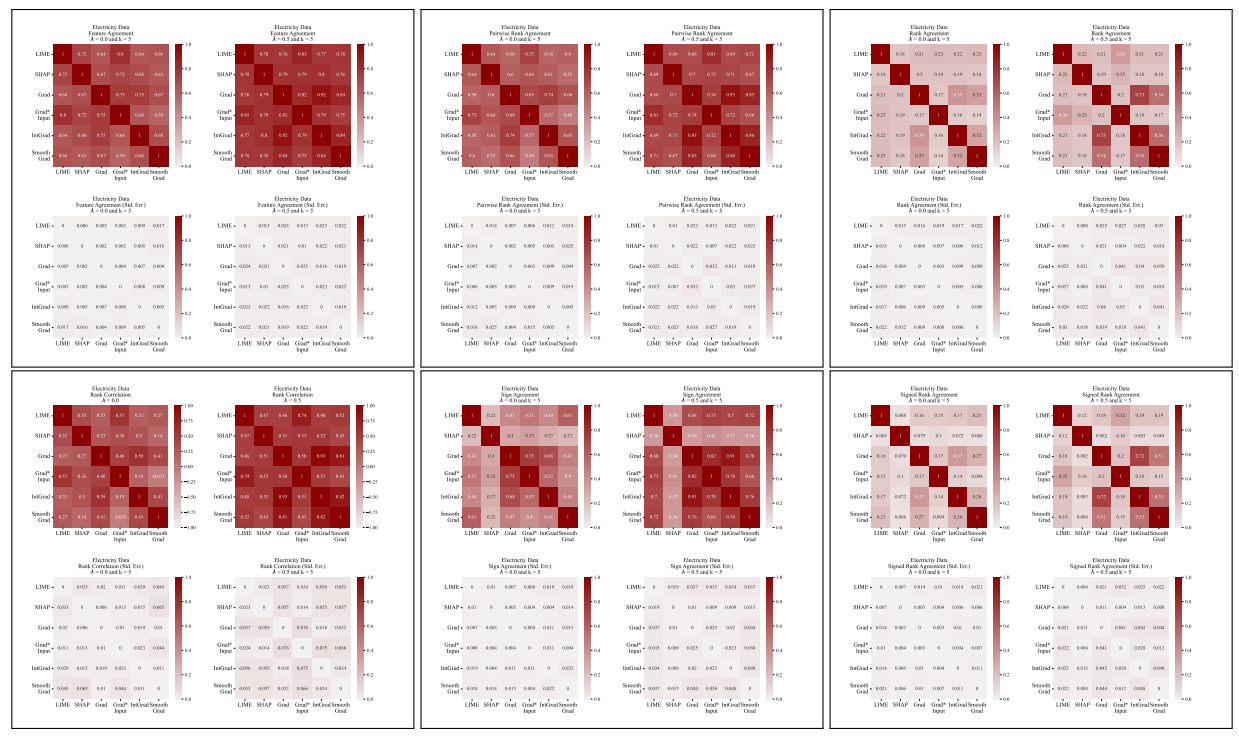
A.5 更多分歧矩阵
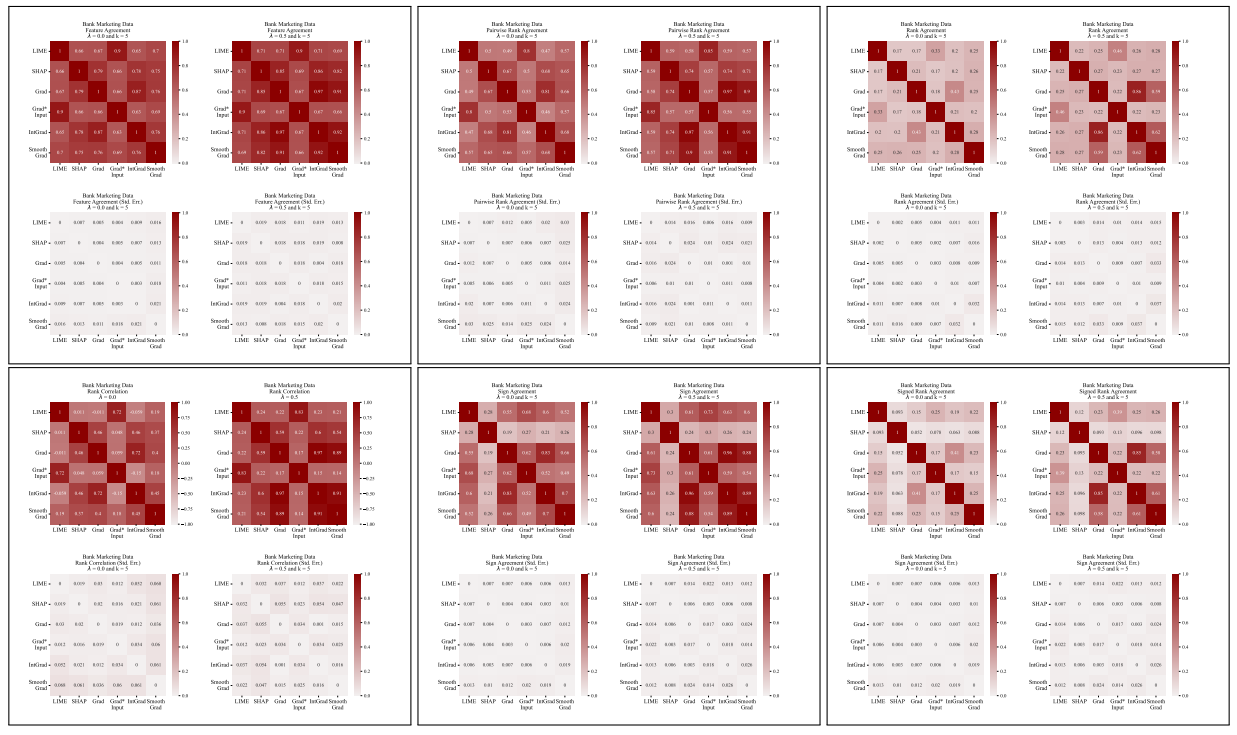
\ 
\ 
A.6 扩展结果
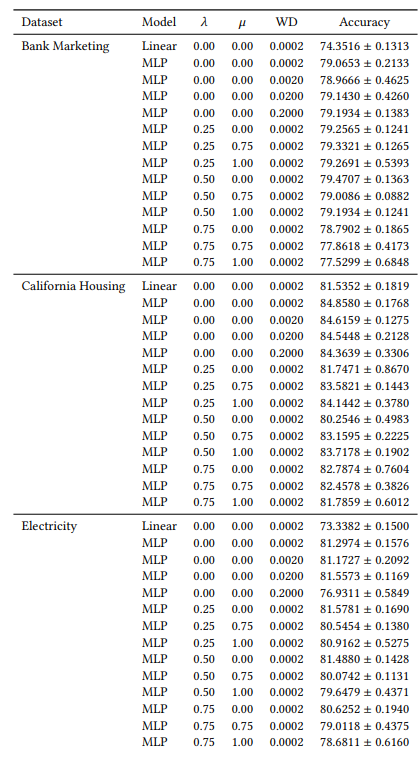
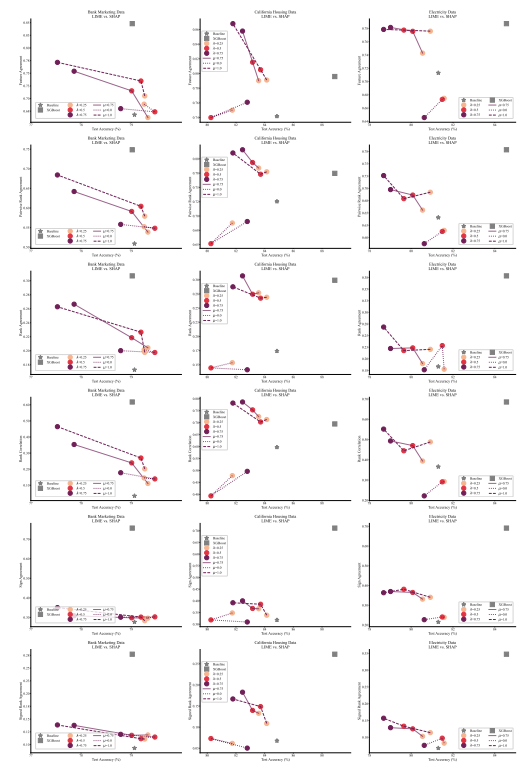
A.7 额外图表
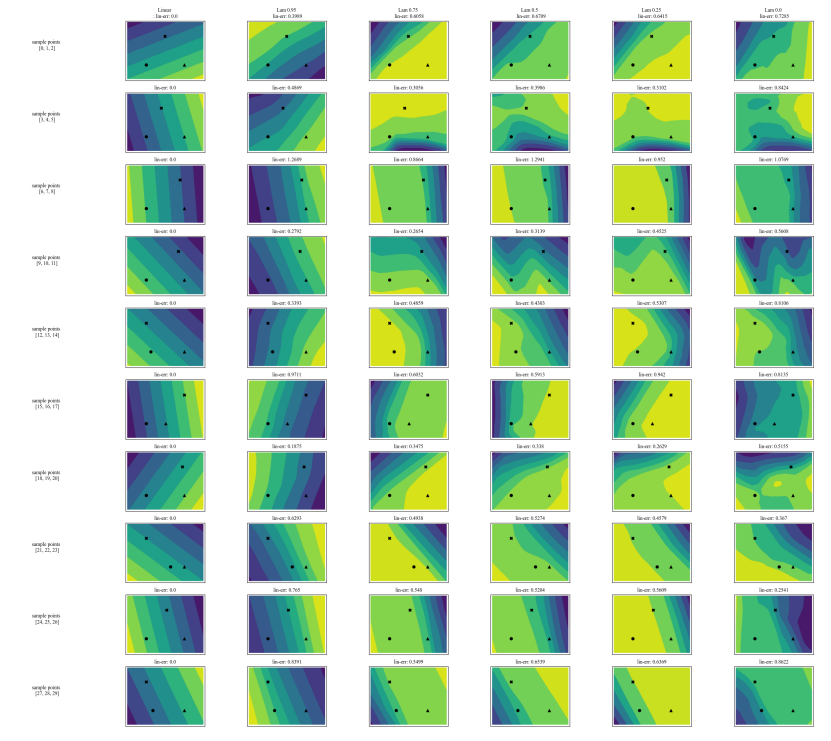
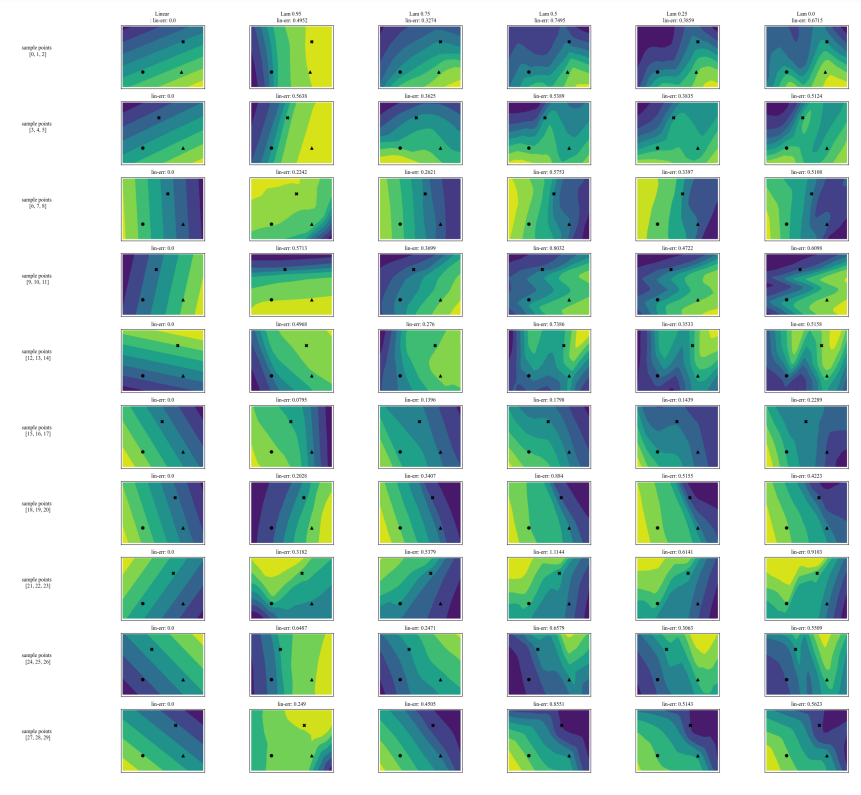
\ 
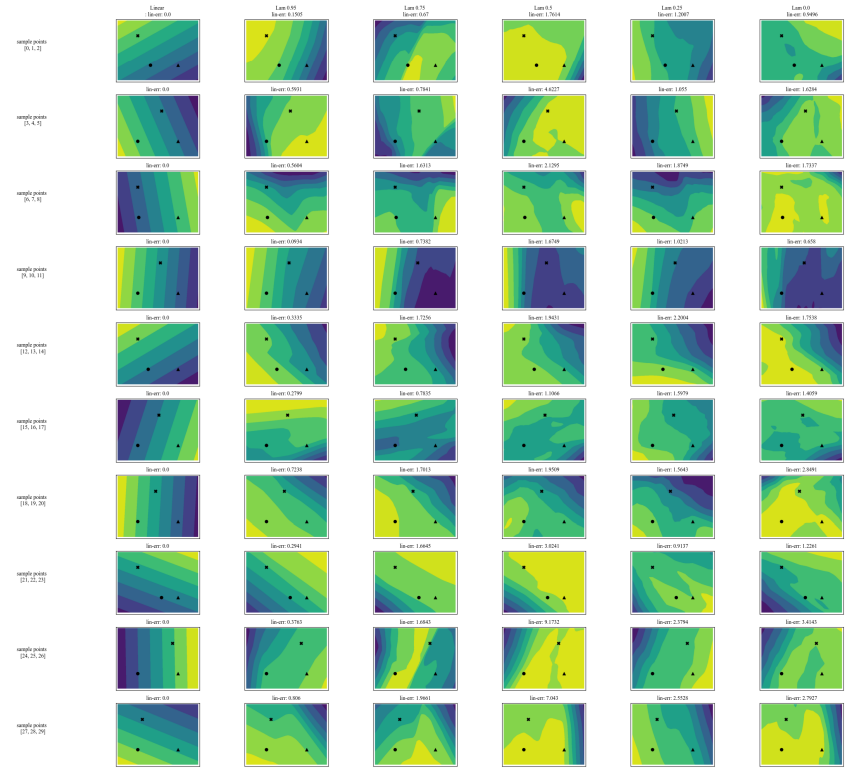
\ 
\ 
\
:::info 作者:
(1) Avi Schwarzschild,马里兰大学帕克分校,马里兰州,美国,以及在Arthur工作期间完成的工作(avi1umd.edu);
(2) Max Cembalest,Arthur,纽约市,纽约州,美国;
(3) Karthik Rao,Arthur,纽约市,纽约州,美国;
(4) Keegan Hines,Arthur,纽约市,纽约州,美国;
(5) John Dickerson†,Arthur,纽约市,纽约州,美国(john@arthur.ai)。
:::
:::info 本论文可在arxiv上获取,采用CC BY 4.0 DEED许可证。
:::
\
您可能也会喜欢

Chainlink 对比 Digitap ($TAP):迈向2026年的实用性和用例比较

SOL 到 Ozak AI 翻转:为什么一些投资者相信 AI 代币具有更高的长期潜力
