无线电偏振数据校准：增强CHIME和Dwingeloo调查之间的相关性

链接目录

摘要和1 引言

1. 法拉第旋转和法拉第合成

2. 数据与仪器

   3.1. CHIME和GMIMS巡天以及3.2. CHIME/GMIMS北部低频段

   3.3. DRAO综合望远镜观测

   3.4. 辅助数据来源

3. 蝌蚪的特征

   4.1. 单频图像中的形态

   4.2. 法拉第深度

   4.3. 法拉第复杂性

   4.4. QU拟合

   4.5. 伪影

4. 蝌蚪的起源

   5.1. 中性氢结构

   5.2. 电离氢结构

   5.3. 候选恒星的自行

   5.4. 法拉第深度和电子柱密度

5. 总结和未来展望

\ 附录

A. 法拉第合成中的已解析和未解析法拉第成分

B. QU拟合结果

\ 参考文献

3.1. CHIME和GMIMS巡天

3.2. CHIME/GMIMS北部低频段

\

\ 我们使用的环形图没有应用波束反卷积。这导致图像中出现一些小伪影，我们将在4.5节中描述，但它们的存在并不妨碍研究几度尺度上的结构，如蝌蚪。在本分析中，我们使用完整CHIME频段的400-729 MHz子集，因为最高频率受到混叠的污染，使得感兴趣区域的图像不可靠。

\ 3.2.1. 极化角校准

\

\

\

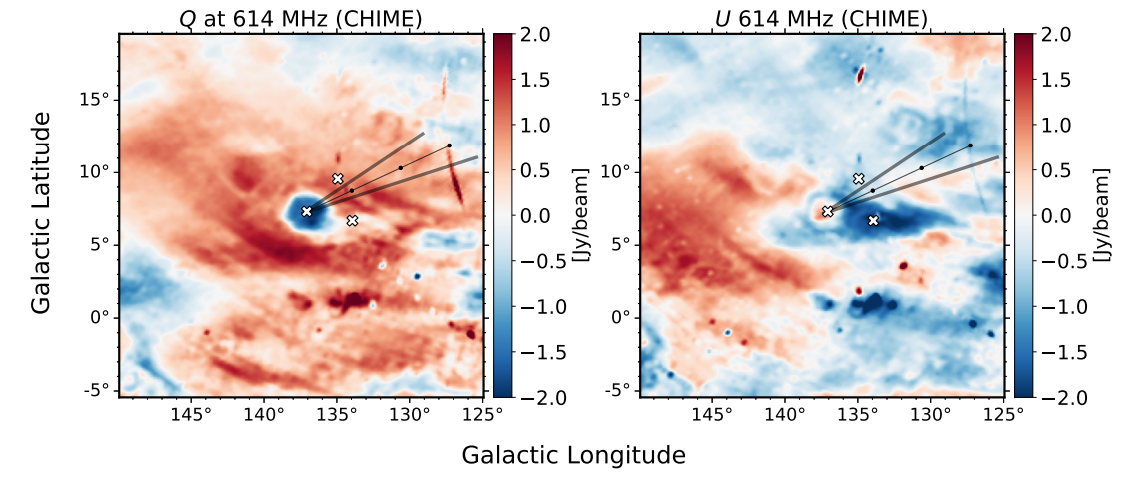
\ 斯托克斯U和V参数是从互相关产物中测量的。我们假设天空中弥散辐射的⟨V⟩=0，因为低密度天体物理环境中的同步辐射不产生圆偏振。V和U之间的泄漏源于相位偏移。我们在每个赤纬和频率处测量平均相移⟨ψ⟩(δ,ν)，假设⟨V⟩=0，并计算

\

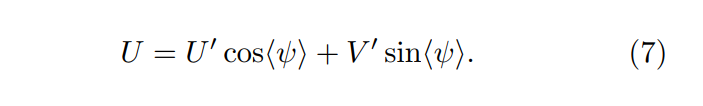
\ ⟨V⟩=0的假设即使在快速射电暴(FRB)观测中也能得到高质量拟合，尽管在这种情况下，该假设的物理依据不如我们研究的弥散极化辐射那么明确(Mckinven等，2023)。我们发现相移与频率呈线性关系，这与弥散辐射的电缆延迟τ=⟨ψ⟩/2πν∼1 ns一致，正如Mckinven等(2021，他们的附录A)在CHIME/FRB数据中发现的那样。

\ 在图1中，我们将校准后的数据与扇区中610 MHz的德温格洛望远镜巡天进行比较(Brouw & Spoelstra 1976)。在有德温格洛数据的方向上，德温格洛U与CHIME U以及德温格洛Q与CHIME Q之间存在强相关性，U-U的相关系数R值为0.91，Q-Q比较的相关系数为0.89。这比未校准的相关系数0.76和0.59分别有显著改善。基于未解析点源测量，我们发现斯托克斯Q中仍有高达20%的泄漏。使用每个点与拟合线之间的平均正交距离，我们发现CHIME和德温格洛数据的噪声描述了图1中约70%的散射。极化角相关性，如图1所示，也通过校准得到改善，大多数离群点是极化强度低的点(黄点)，这些点导出的χ具有较高的不确定性。

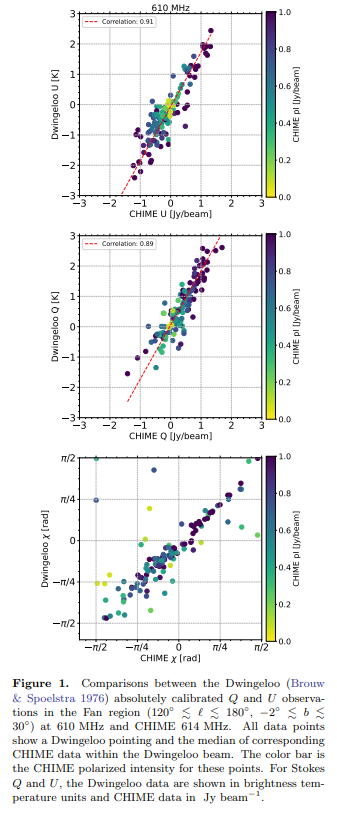
\ 我们在图2中展示了CHIME Q和U图，其中χ=0参考轴旋转到北银极。虽然我们的数据中存在斯托克斯I到Q的泄漏，但蝌蚪结构不可能仅仅是泄漏的结果。尽管整个扇区(包括蝌蚪)都有总强度辐射，但这种辐射在小尺度上没有特征，因此不能产生与蝌蚪形态匹配的虚假极化。此外，蝌蚪不可能是源自大角距离(如银河平面)并在远侧瓣中看到的斯托克斯I辐射的产物。虽然远侧瓣的极化特性较差，但它们的极化在相当大的区域内平均为低值。此外，使用线性馈源时，I的泄漏主要进入Q，而不是U(在CHIME的本地赤道坐标中)，但蝌蚪在赤道坐标的斯托克斯U中已经明显可见(未显示)。

\

\

\ 3.2.2. CHIME数据的法拉第合成

\

\

\ 使用RM-Tools中的rmtools_peakfitcube算法，我们获得了峰值法拉第深度及其

\

\ 沿所有视线的每个光谱的相关误差。结果图显示在图3b中。我们使用峰值法拉第深度而非一阶矩(Dickey等，2019)，以关注每个视线中最亮特征的法拉第深度，而不是法拉第复杂区域中的加权平均法拉第深度。

\ 我们在图3a中展示了法拉第深度光谱的积分极化强度作为零阶矩图。图3c显示了由每个像素的峰值法拉第深度去旋转到χ0的极化角图。

\

:::info 作者：

(1) Nasser Mohammed，不列颠哥伦比亚大学计算机科学、数学、物理与统计系，奥肯那根校区，基洛纳，BC V1V 1V7，加拿大和多米尼恩射电天体物理天文台，赫兹伯格天文学与天体物理学研究中心，加拿大国家研究委员会，邮政信箱248，彭蒂克顿，BC V2A 6J9，加拿大；

(2) Anna Ordog，不列颠哥伦比亚大学计算机科学、数学、物理与统计系，奥肯那根校区，基洛纳，BC V1V 1V7，加拿大和多米尼恩射电天体物理天文台，赫兹伯格天文学与天体物理学研究中心，加拿大国家研究委员会，邮政信箱248，彭蒂克顿，BC V2A 6J9，加拿大；

(3) Rebecca A. Booth，卡尔加里大学物理与天文系，2500大学道西北，卡尔加里，艾伯塔省，T2N 1N4，加拿大；

(4) Andrea Bracco，INAF – 阿切特里天体物理天文台，Largo E. Fermi 5，50125佛罗伦萨，意大利和巴黎高等师范学院物理实验室，ENS，巴黎科学艺术文学大学，法国国家科学研究中心，索邦大学，巴黎大学，F-75005巴黎，法国；

(5) Jo-Anne C. Brown，卡尔加里大学物理与天文系，2500大学道西北，卡尔加里，艾伯塔省，T2N 1N4，加拿大；

(6) Ettore Carretti，INAF-射电天文研究所，Via Gobetti 101，40129博洛尼亚，意大利；

(7) John M. Dickey，塔斯马尼亚大学自然科学学院，霍巴特，塔斯马尼亚7000，澳大利亚；

(8) Simon Foreman，亚利桑那州立大学物理系，坦佩，亚利桑那州85287，美国；

(9) Mark Halpern，不列颠哥伦比亚大学物理与天文系，6224农业路，温哥华，BC V6T 1Z1，加拿大；

(10) Marijke Haverkorn，拉德堡德大学天体物理学/IMAPP系，邮政信箱9010，6500 GL奈梅亨，荷兰；

(11) Alex S. Hill，不列颠哥伦比亚大学计算机科学、数学、物理与统计系，奥肯那根校区，基洛纳，BC V1V 1V7，加拿大和多米尼恩射电天体物理天文台，赫兹伯格天文学与天体物理学研究中心，加拿大国家研究委员会，邮政信箱248，彭蒂克顿，BC V2A 6J9，加拿大；

(12) Gary Hinshaw，不列颠哥伦比亚大学物理与天文系，6224农业路，温哥华，BC V6T 1Z1，加拿大；

(13) Joseph W. Kania，西弗吉尼亚大学物理与天文系，邮政信箱6315，摩根敦，西弗吉尼亚州26506，美国和西弗吉尼亚大学引力波与宇宙学中心，栗树岭研究大楼，摩根敦，西弗吉尼亚州26505，美国；

(14) Roland Kothes，多米尼恩射电天体物理天文台，赫兹伯格天文学与天体物理学研究中心，加拿大国家研究委员会