集合论中"乘积"和相等性的逻辑内涵
链接目录
摘要
- 致谢与引言
2. 泛性质
3. 实践中的积
4. 代数几何中的泛性质
5. Grothendieck使用等式的问题
6. 关于"典范"映射的更多内容
7. 更高级数学中的典范同构
8. 总结与参考文献
泛性质
我了解到数学基础有三类合理的体系:基于集合论的、基于类型论的和基于范畴论的。也有各种结果表明,广义上讲,这些基础能够证明相同的定理。然而,要讨论相等性,我们必须确切地确定我们所讨论的内容,因此我将选择ZFC集合论和经典逻辑作为我们讨论的基础。1
做出这一决定的基础很简单:如果一个数学家曾经上过关于其学科逻辑基础的课程(而许多人没有),那么这很可能是一门集合论课程。此外,纯数学文献是以表面上的集合论风格写成的:我们被告知群是具有某些结构和公理的集合,流形是具有不同结构和公理的集合,等等。这里"集合"一词只是"原子集合"这一概念的占位符。
显然,相等的两个集合具有相同的元素;这源于所谓的相等替换原则,该原则指出,如果X和Y是任何两个相等的数学对象,那么你在基础系统中关于X的任何陈述对Y也成立。反之,具有相同元素的两个集合是相等的,这被作为理论的一个公理强加。这确保了集合的抽象概念与我们对其所代表内容的心理模型相符:集合不多不少就是一个东西的集合。
现在我想开始讨论唯一表征数学对象的性质。让我们从一个例子开始:两个集合X和Y的积X × Y。我现在要警告读者,在接下来的几段中,我将非常仔细地区分X和Y的积的概念与X和Y的一个积的概念。两个集合的积X × Y被定义为有序对(x, y)的集合,其中x ∈ X且y ∈ Y(可以使用集合论的公理检查创建这个集合是可能的)。
注意,这里我们遇到了与实数相同的问题:在集合论中有几种不同的方式来定义有序对的概念。集合论设计得非常适合处理无序对:集合{x, y}和{y, x}具有相同的元素,因此是相等的,所以要定义有序对,需要使用某种技巧。
维基百科关于有序对的页面[Wik04b]目前给出了三种不同的构造,分别归功于Wiener({{{x}, ∅}, {{y}}})、Hausdorff({{x, 1}, {y, 2}})和Kurotowski({{x}, {x, y}});这些都显得有些人为。2 数学家们再次清楚地知道,这个问题在实践中根本不重要:我们只需要知道有序对的定义性质,即(x1, y1) = (x2, y2) ⇐⇒ x1 = x2且y1 = y2;这就是我们所需要的全部,而所有定义都满足这一性质。
积X × Y配备了两个投影映射π1 : X × Y → X和π2 : X × Y → Y。严格来说,不仅仅是积,而是三元组(X × Y, π1, π2)满足以下泛性质:
积的泛性质:如果三元组(P, π1 : P → X, π2 : P → Y)满足以下性质,则称其为X和Y的一个积:如果S是任何集合,且f : S → X和g : S → Y是函数,则存在唯一的从S到P的函数,使得它与π1的复合是f,与π2的复合是g。
泛性质不是两个集合积的定义;它可以被视为积需要满足的无限多个事实(对于每个集合S和函数f和g的选择都有一个)。验证X和Y的积X × Y,配备自然投影,是一个积并不难。但反过来却完全不成立:通常有很多其他三元组(P, π1, π2)满足作为积的性质,而不是那个积。
例如,如果X = {37}且Y = {42},则积X × Y是{(37, 42)},但实际上任何具有一个元素的集合P,配备π1 : P → X将所有内容映射到37和π2 : P → Y将所有内容映射到42,都满足作为积的泛性质。特别是,通常有不可数多的不同事物满足作为积的性质。然而,数学家们非常擅长识别这些不同的事物;它们在超越=符号正确用法的方式上是"相同的"。我们可以这样做是因为泛对象的唯一性瑜伽。让我们在积的情况下通过这个瑜伽,这是一段形式化的范畴论废话。
假设P1和P2都是X和Y的一个积。将P2的泛性质的存在部分(及其到X和Y的投影)应用于集合S = P1(及其到X和Y的投影)给我们一个函数α : P1 → P2,它与到X和Y的投影交换。在论证中交换1和2,我们也可以构造一个函数β : P2 → P1,它与投影交换。此外,β ◦ α是从P1到P1的映射,与投影交换,恒等函数也是如此;通过P1应用于P1的泛性质的唯一性部分,我们推断β ◦ α必须是P1上的恒等映射;同样,α ◦ β必须是P2上的恒等映射。
因此α和β是与投影映射交换的双射。最后,使用P2应用于P1的泛性质的唯一性部分告诉我们,α是从P1到P2的唯一与投影交换的映射,通过对称性,β是从P2到P1的唯一与投影交换的映射。这种抽象废话(从未提及任何集合的元素,只有对象和态射)的结果是,在P1和P2之间存在唯一的互逆双射,它们与到因子X和
Y的投影交换。特别是,如果P是X和Y的一个积,那么它以与投影兼容的方式唯一同构于X和Y的积X × Y。在我们的一元素例子X = {37}和Y = {42}中,如果P是任何一元素集,那么从P到X × Y的唯一映射当然将该元素映射到(37, 42)。
:::info 作者: KEVIN BUZZARD
:::
:::info 本论文可在arxiv上获取,采用CC BY 4.0 DEED许可证。
:::
\
您可能也会喜欢

变盘前夕:比特币是冲高96500再回落还是直接下探86000?

Solana Treasury Stocks: 为什么这些公司正在大量购买SOL?
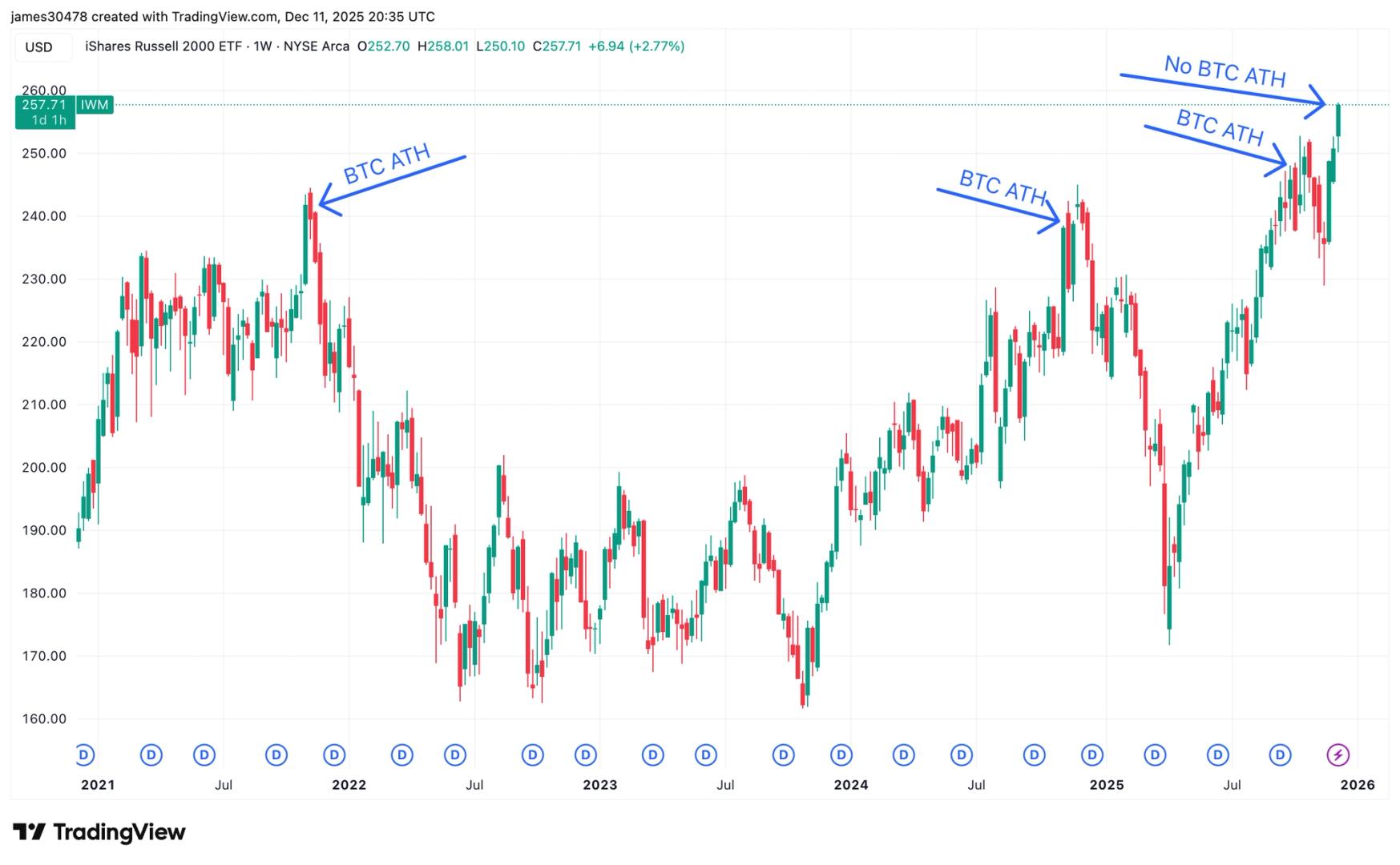
从同步到滞后,比特币准备追赶小盘股高点
复制链接X (Twitter)LinkedIn脸书电子邮件