How Scientists Taught AI to Handle Shock Waves

Table of Links

Abstract and 1. Introduction

1.1. Introductory remarks

1.2. Basics of neural networks

1.3. About the entropy of direct PINN methods

1.4. Organization of the paper

1. Non-diffusive neural network solver for one dimensional scalar HCLs

   2.1. One shock wave

   2.2. Arbitrary number of shock waves

   2.3. Shock wave generation

   2.4. Shock wave interaction

   2.5. Non-diffusive neural network solver for one dimensional systems of CLs

   2.6. Efficient initial wave decomposition

2. Gradient descent algorithm and efficient implementation

   3.1. Classical gradient descent algorithm for HCLs

   3.2. Gradient descent and domain decomposition methods

3. Numerics

   4.1. Practical implementations

   4.2. Basic tests and convergence for 1 and 2 shock wave problems

   4.3. Shock wave generation

   4.4. Shock-Shock interaction

   4.5. Entropy solution

   4.6. Domain decomposition

   4.7. Nonlinear systems

4. Conclusion and References

4.1. Practical implementations

This subsection is devoted to the practical aspects of the training process of neural networks. The implementation of the algorithms above is performed using the library neural network jax, see [26]. Although the algorithms look complex, they are actually very easy to implement using jax and we did not face any difficulty in the tuning of the hyper-parameters. In this paper we propose a proof-of-concept of a novel method in low dimension, and which ultimately deals with simple (piecewise-)smooth functions. As a consequence, we have not addressed in details questions related to the choice of the optimization algorithm or of the hyper-parameters, because in this setting they are not particularly relevant. In our numerical simulations we have considered tanh neural networks with one or two hidden layers. The learning nodes to approximate the PDE residuals are randomly selected in the rectangular regions R = (0, 1) × (0, T) (see Subsection 2.1). The weights λ, µ in (12) and (21) are taken equal to 1/2, and more generally for equations with several shock waves or for systems, an equal weight is given to each contribution of the loss functions. Moreover the neural

\

\ In all the numerical experiments below we consider the problem (1a)-(1b), and in the following experiments we only specify Ω × [0, T], f(u) and u0. We refer to the results with our algorithms as NDNN solution.

4.2. Basic tests and convergence for 1 and 2 shock wave problems

In this subsection, we do not consider any domain decomposition, so that only one global loss function is minimized as described in Subsections 2.1, 2.2.

\ Experiment 1. In this experiment we consider Ω × [0, T] = (−4, 1) × [0, 3/4] with f(u) = 4u(2 − u). The initial data is given by

\ \

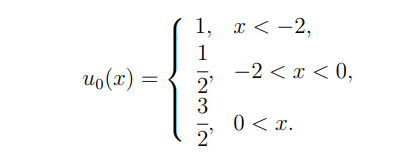
\ \ In the time interval [0, 1/2], it is constituted by a rarefaction and a shock wave with constant velocity. Then, in the time interval [1/2, 3/4] the initial shock wave interacts with the rarefaction wave to produce a new shock with non-constant velocity. More specifically the solution is given by

\ \

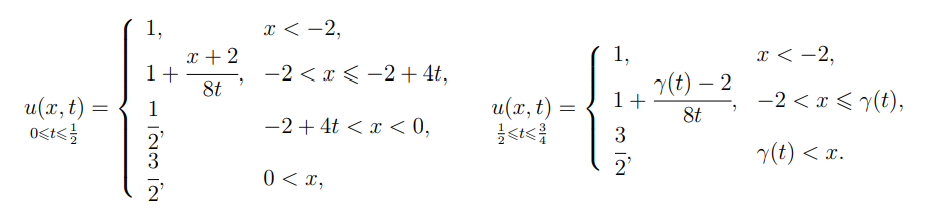
\ \ Here γ is the DL and it solves

\ \

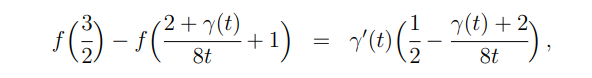
\ \ for t ∈ [1/2, 1] and γ(1/2) = 0.

\ \

\ \ \

\ \ \

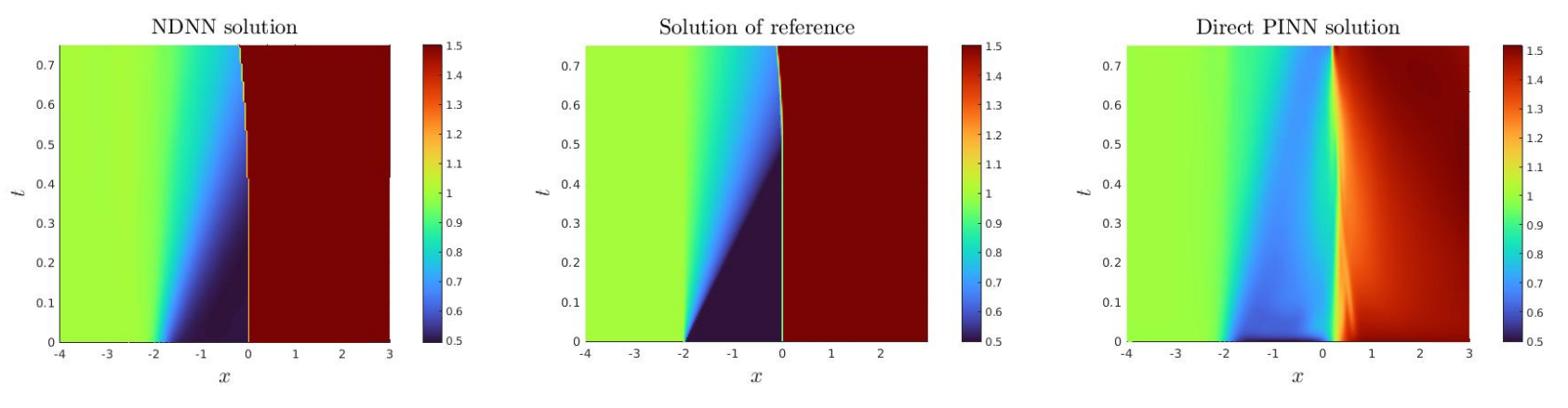
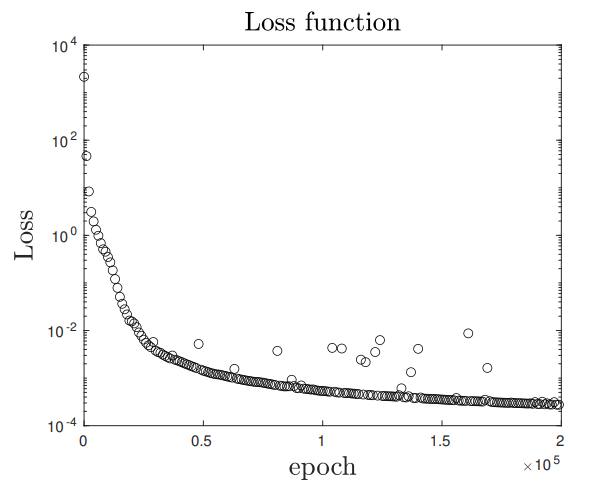
\ \ Let us mention that using the same numerical data, a direct PINN algorithm provides a very inaccurate approximation of the stationary then non-stationary shock waves, while our algorithm provides accurate approximations. This last point is discussed in the 2 following tests.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \ \

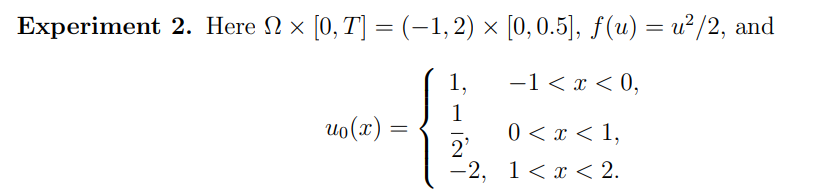
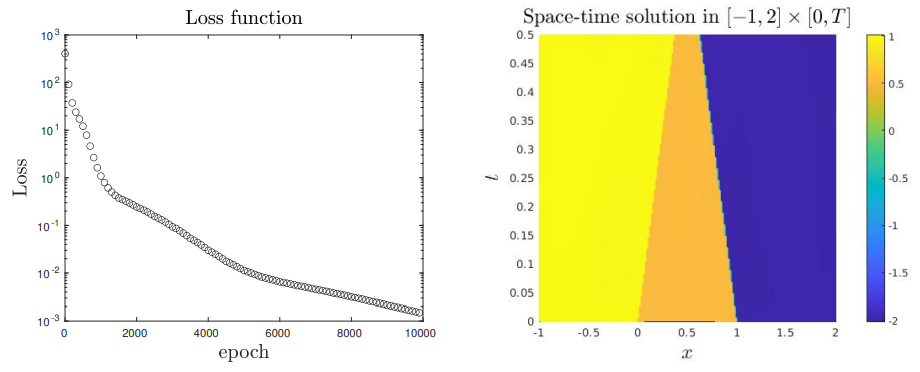
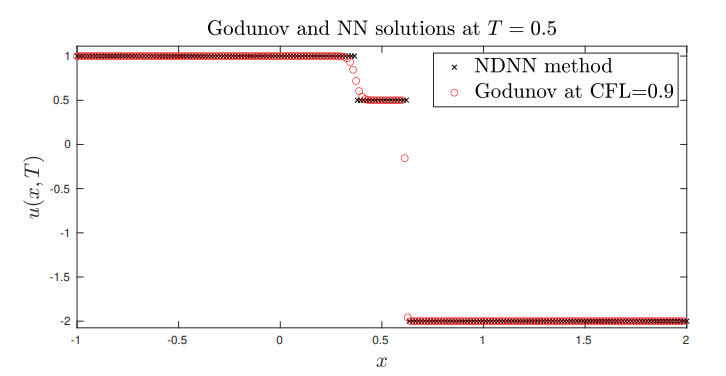
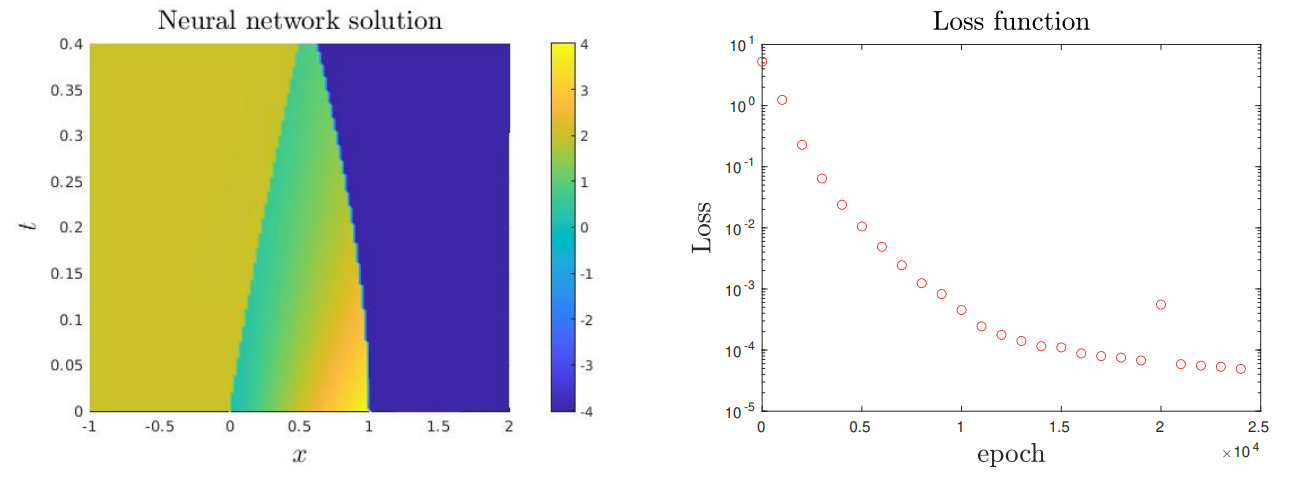
\ \ These experiments allow to validate the convergence of the proposed approach.

\

:::info Authors:

(1) Emmanuel LORIN, School of Mathematics and Statistics, Carleton University, Ottawa, Canada, K1S 5B6 and Centre de Recherches Mathematiques, Universit´e de Montr´eal, Montreal, Canada, H3T 1J4 (elorin@math.carleton.ca);

(2) Arian NOVRUZI, a Corresponding Author from Department of Mathematics and Statistics, University of Ottawa, Ottawa, ON K1N 6N5, Canada (novruzi@uottawa.ca).

:::

:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.

:::

\