Offline Generative Active Learning: Feasibility and Limitations

Table of Links

Abstract and 1 Introduction

1. Related work

   2.1. Generative Data Augmentation

   2.2. Active Learning and Data Analysis

2. Preliminary

3. Our method

   4.1. Estimation of Contribution in the Ideal Scenario

   4.2. Batched Streaming Generative Active Learning

4. Experiments and 5.1. Offline Setting

   5.2. Online Setting

5. Conclusion, Broader Impact, and References

   \

A. Implementation Details

B. More ablations

C. Discussion

D. Visualization

5. Experiments

First, we perform some analytical experiments in an offline setting(as discussed in Remark 4.6) to verify the feasibility of our method and also to facilitate a better understanding of our method for readers. Then, we conduct the main experiments under the online setting, compared with our baseline. Key ablation studies are also conducted to substantiate the efficiency of our method. Detailed information about the implementation can be found in Appendix A.

5.1. Offline Setting

5.1.1. CIFAR-10

\

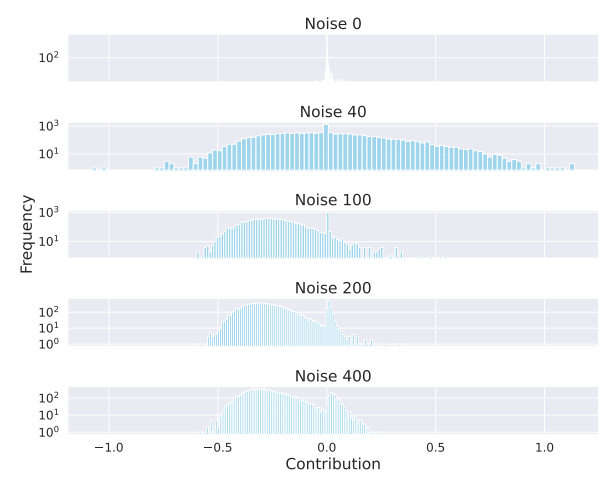
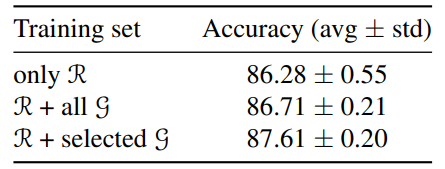
\ As shown in Figure 2, it is observable that with the escalating scale of noise, the distribution of contributions progressively shifts to the left. This indicates that excessive noise tends to negatively impact the model. Note that the split with a noise of 0 is our training set, so we can see that the contribution values of these samples are concentrated around zero. In other words, these samples can no longer bring positive effects to the model because they have been fully utilized in previous training. This observation is consistent with some previous active learning work (Cai et al., 2013; Ash et al., 2021; Saran et al., 2023), where they also estimate the amount of information or the difficulty level of samples through gradients. However, they do not consider the positive or negative contributions but only select samples with larger absolute values. We further conduct quantitative experiments, as shown in Table 1, to prove that using our method to select data can effectively improve the

\

\

\ performance of the model.

\ 5.1.2. LVIS

\

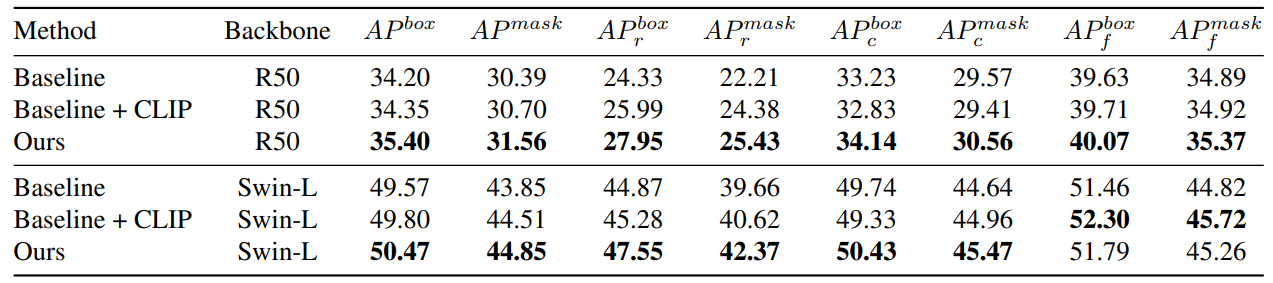
\ This gradient then serves to estimate each instance’s contribution. Subsequently, we rank these instances in decreasing order of their contribution, facilitating per-image analysis. As an illustrative example, we use a ‘bun’ category from the LVIS, because we discover that Stable Diffusion does not perform optimally within this category, often leading to confusion between ‘bun’ and ‘bunny’, thereby resulting in the generation of ambiguous data. As depicted in Figure 3, it can be observed that the instances having the most significant contributions are nearly unambiguous, whereas the instances with minimal contributions are mostly incorrect, resulting in rabbit images being generated. Therefore, through our method, we can effectively filter out the generated data with ambiguity.

\ To verify the indispensability of online learning, we first use the offline method to filter the generated data for training and compare it with our baseline. As shown in Figure 4, the offline method can only bring a slight improvement to the

\

\

\ final model performance. In addition, in the early stage of model training, this performance improvement is still quite obvious, but with the training process, this performance improvement gradually diminishes. We conjecture that this trend is likely due to the offline contribution estimation’s reliance on the initial model, and as the model undergoes training, the parameters change significantly, which leads to the inaccuracy of the offline contribution estimation. Therefore, the necessity arises for online contribution estimation.

\

:::info Authors:

(1) Muzhi Zhu, with equal contribution from Zhejiang University, China;

(2) Chengxiang Fan, with equal contribution from Zhejiang University, China;

(3) Hao Chen, Zhejiang University, China (haochen.cad@zju.edu.cn);

(4) Yang Liu, Zhejiang University, China;

(5) Weian Mao, Zhejiang University, China and The University of Adelaide, Australia;

(6) Xiaogang Xu, Zhejiang University, China;

(7) Chunhua Shen, Zhejiang University, China (chunhuashen@zju.edu.cn).

:::

:::info This paper is available on arxiv under CC BY-NC-ND 4.0 Deed (Attribution-Noncommercial-Noderivs 4.0 International) license.

:::

\