交易所DEX+

抽金磚 & BTC2000g

我們使用原始來自 OpenML 的表格數據集，並由 HuggingFace 上的 Inria-Soda 團隊編譯成一組基準數據集。我們在 28,855 個訓練樣本上進行訓練，並在剩餘的 9,619 個樣本上進行測試。所有的 MLP 都使用批次大小為 64、64 和 0,0005 進行訓練，我們研究了每層有 100 個神經元的 3 層結構。我們在此定義了我們工作中使用的六大指標。我們使用原始來自 OpenML 的表格數據集，並由 HuggingFace 上的 Inria-Soda 團隊編譯成一組基準數據集。我們在 28,855 個訓練樣本上進行訓練，並在剩餘的 9,619 個樣本上進行測試。所有的 MLP 都使用批次大小為 64、64 和 0,0005 進行訓練，我們研究了每層有 100 個神經元的 3 層結構。我們在此定義了我們工作中使用的六大指標。

極客的機器學習實驗指南

2025/09/21 13:47

連結表格

摘要和1. 引言

1.1 事後解釋

1.2 分歧問題

1.3 鼓勵解釋共識

相關工作
Pear: 事後解釋器一致性正則化器
共識訓練的效果

4.1 一致性指標

4.2 改善共識指標

[4.3 一致性的代價是什麼?]()

4.4 解釋是否仍然有價值?

4.5 共識與線性

4.6 兩個損失項
討論

5.1 未來工作

5.2 結論、致謝和參考文獻

附錄

A 附錄

A.1 數據集

在我們的實驗中，我們使用了最初來自OpenML的表格數據集，這些數據集由Inria-Soda團隊編譯成HuggingFace上的基準數據集[11]。我們提供每個數據集的一些詳細信息：

\ 銀行營銷 這是一個二元分類數據集，具有六個輸入特徵，並且大致類別平衡。我們在7,933個訓練樣本上進行訓練，並在剩餘的2,645個樣本上進行測試。

\ 加州房價 這是一個二元分類數據集，具有七個輸入特徵，並且大致類別平衡。我們在15,475個訓練樣本上進行訓練，並在剩餘的5,159個樣本上進行測試。

\ 電力這是一個二元分類數據集，具有七個輸入特徵，並且大致類別平衡。我們在28,855個訓練樣本上進行訓練，並在剩餘的9,619個樣本上進行測試。

A.2 超參數

我們的許多超參數在所有實驗中都是恆定的。例如，所有MLP都使用64的批量大小和0.0005的初始學習率進行訓練。此外，我們研究的所有MLP都有3個隱藏層，每層100個神經元。我們始終使用AdamW優化器[19]。訓練的輪數因情況而異。對於所有三個數據集，當𝜆∈{0.0, 0.25}時，我們訓練30個輪次，否則訓練50個輪次。在訓練線性模型時，我們使用10個輪次和0.1的初始學習率。

A.3 分歧指標

我們在此定義我們工作中使用的六個一致性指標。

\ 前四個指標取決於每個解釋中最重要的前k個特徵。讓𝑡𝑜𝑝_𝑓 𝑒𝑎𝑡𝑢𝑟𝑒𝑠(𝐸, 𝑘)表示解釋𝐸中最重要的前k個特徵，讓𝑟𝑎𝑛𝑘 (𝐸, 𝑠)是特徵𝑠在解釋𝐸中的重要性排名，讓𝑠𝑖𝑔𝑛(𝐸, 𝑠)是特徵𝑠在解釋𝐸中重要性分數的符號（正、負或零）。

\ 接下來的兩個一致性指標取決於每個解釋中的所有特徵，而不僅僅是前k個。讓𝑅是一個根據重要性計算解釋中特徵排名的函數。

\ （注意：Krishna等人[15]在他們的論文中指出，𝐹應該是由最終用戶指定的一組特徵，但在我們的實驗中，我們使用此指標的所有特徵）。

A.4 垃圾特徵實驗結果

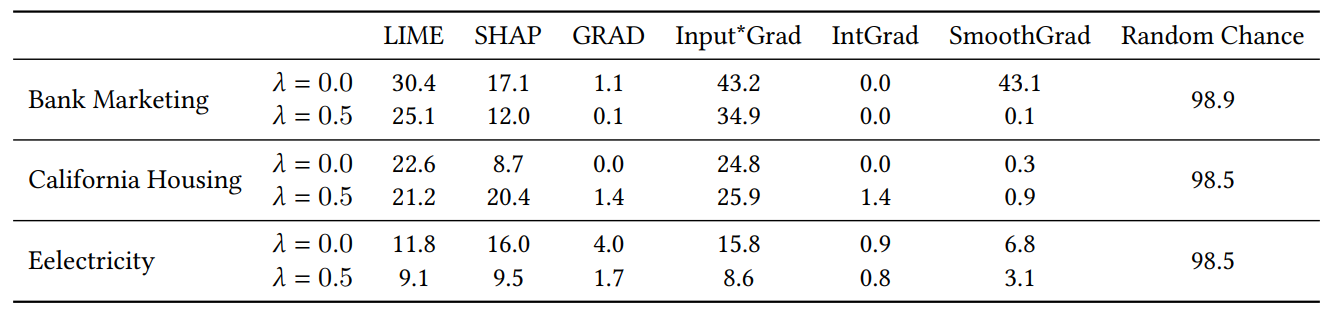
當我們為第4.4節的實驗添加隨機特徵時，我們將特徵數量增加到了兩倍。我們這樣做是為了檢查我們的共識損失是否會通過比自然訓練的模型更頻繁地將不相關特徵放在前K位來損害解釋質量。在表1中，我們報告了每個解釋器在前5個最重要特徵中包含一個隨機特徵的時間百分比。我們觀察到，在整個範圍內，我們沒有看到這些百分比在𝜆 = 0.0（沒有我們共識損失的基準MLP）和𝜆 = 0.5（使用我們共識損失訓練的MLP）之間有系統性增加

\ 表1：垃圾特徵獲得前5名排名的頻率，以百分比計量。

A.5 更多分歧矩陣

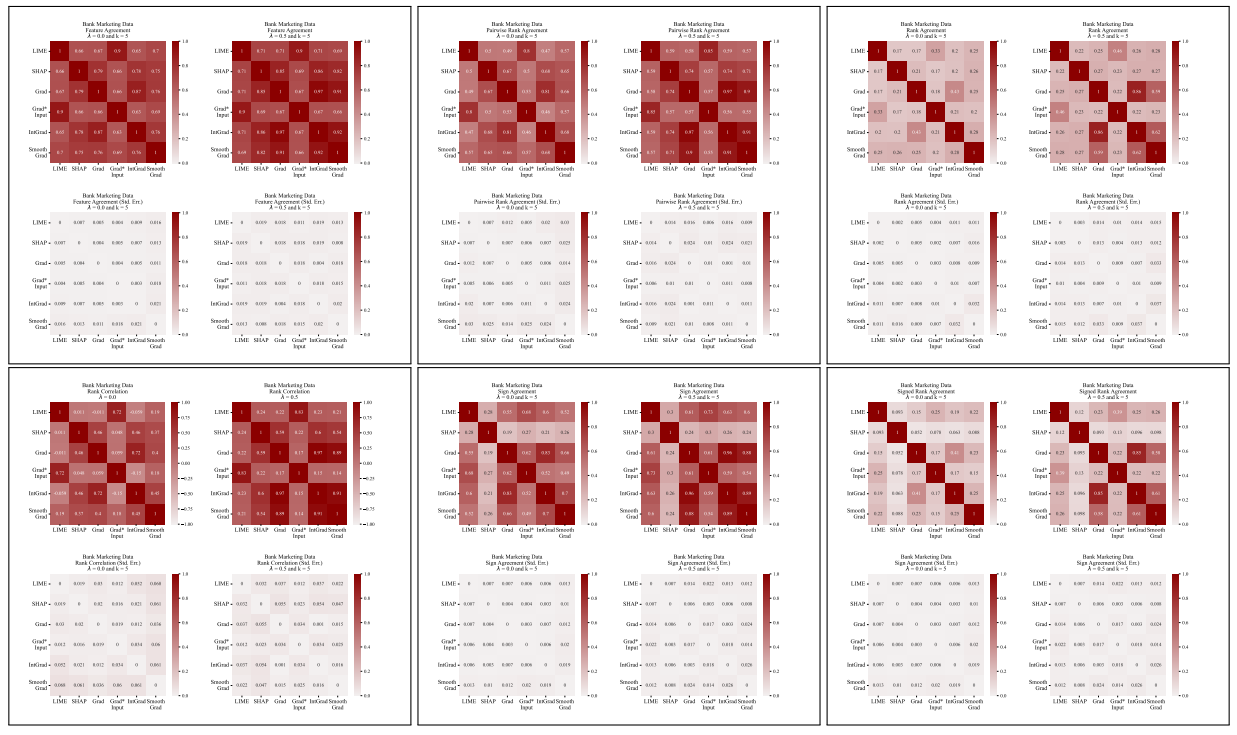
圖9：本文考慮的所有指標在銀行營銷數據上的分歧矩陣。

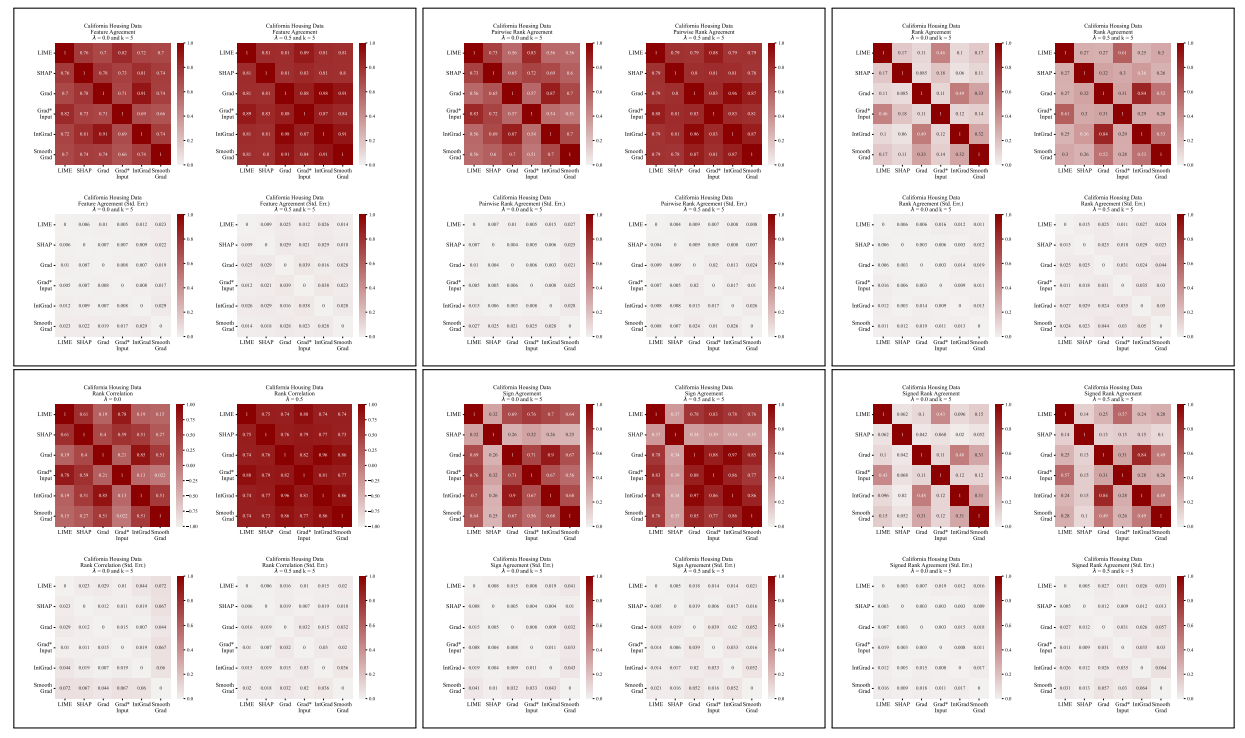
\ 圖10：本文考慮的所有指標在加州房價數據上的分歧矩陣。

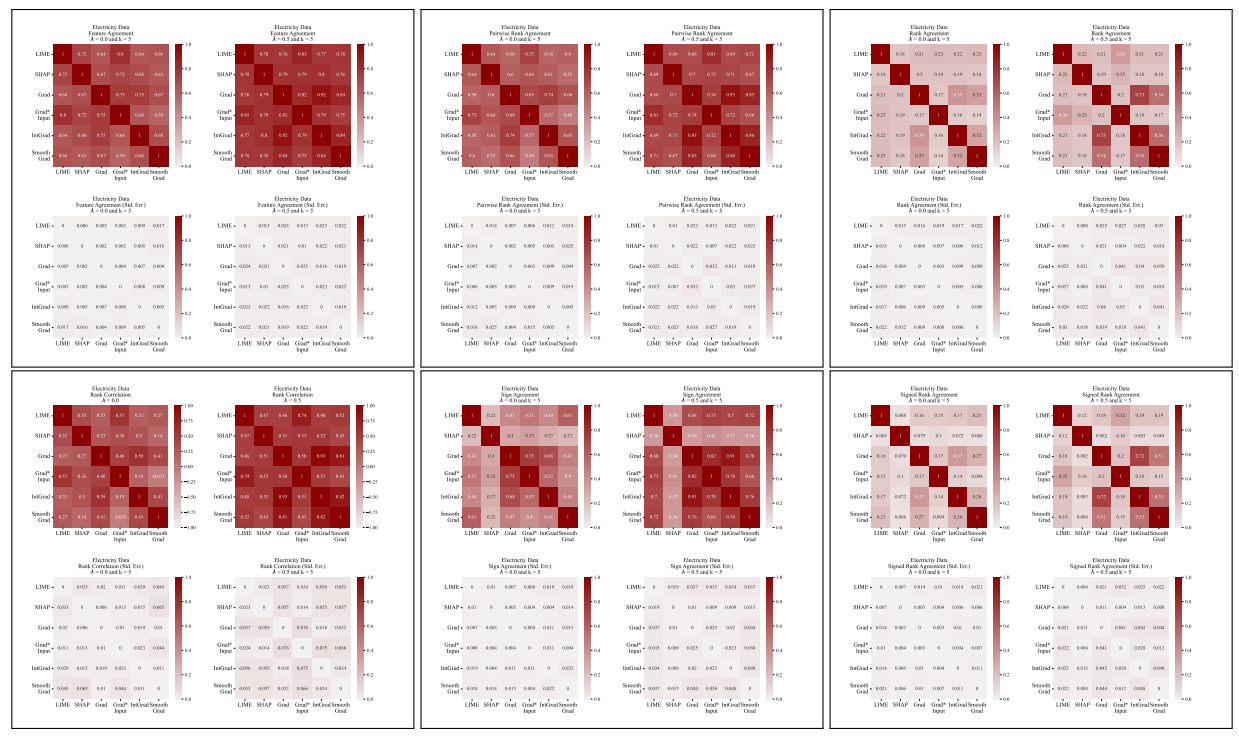
\ 圖11：本文考慮的所有指標在電力數據上的分歧矩陣。

A.6 擴展結果

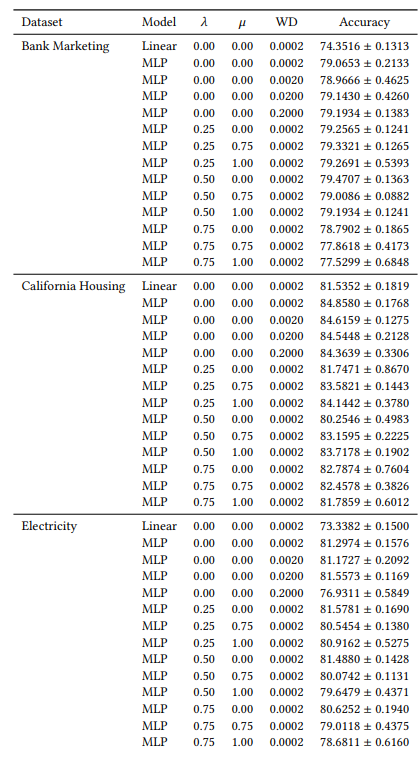
表2：我們訓練的模型的平均測試準確率。此表按數據集、模型、損失中的超參數和權重衰減係數（WD）組織。平均值是通過多次試驗計算的，我們報告平均值±一個標準誤差。

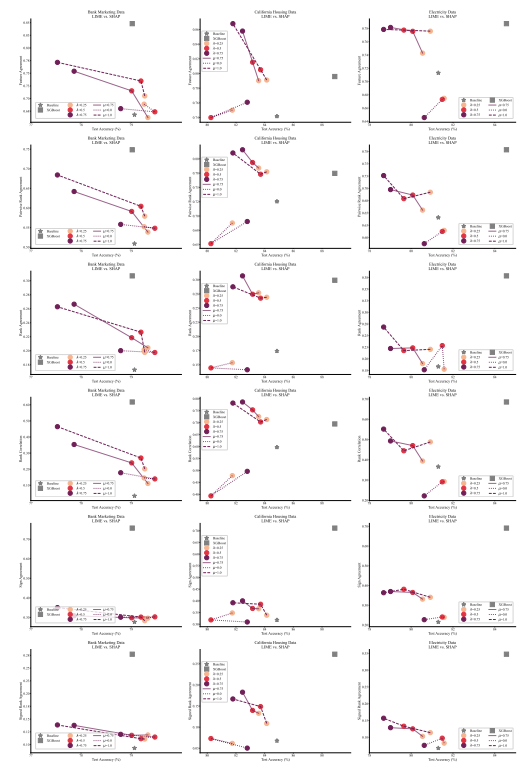
A.7 額外圖表

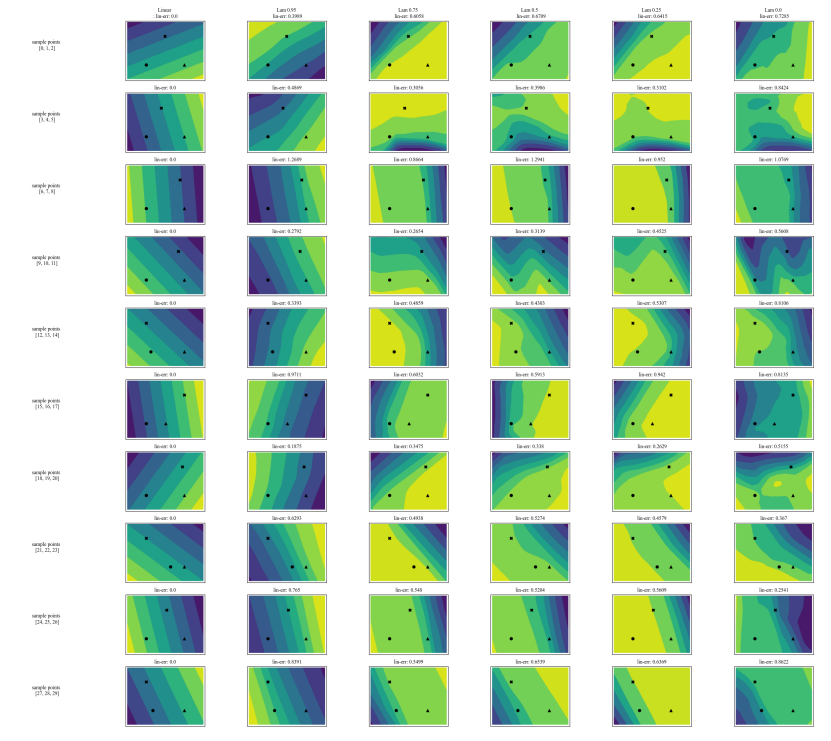
圖12：MLP的logit曲面，每個都使用不同的lambda值訓練，在來自銀行營銷數據集的10個隨機構建的三點平面上。

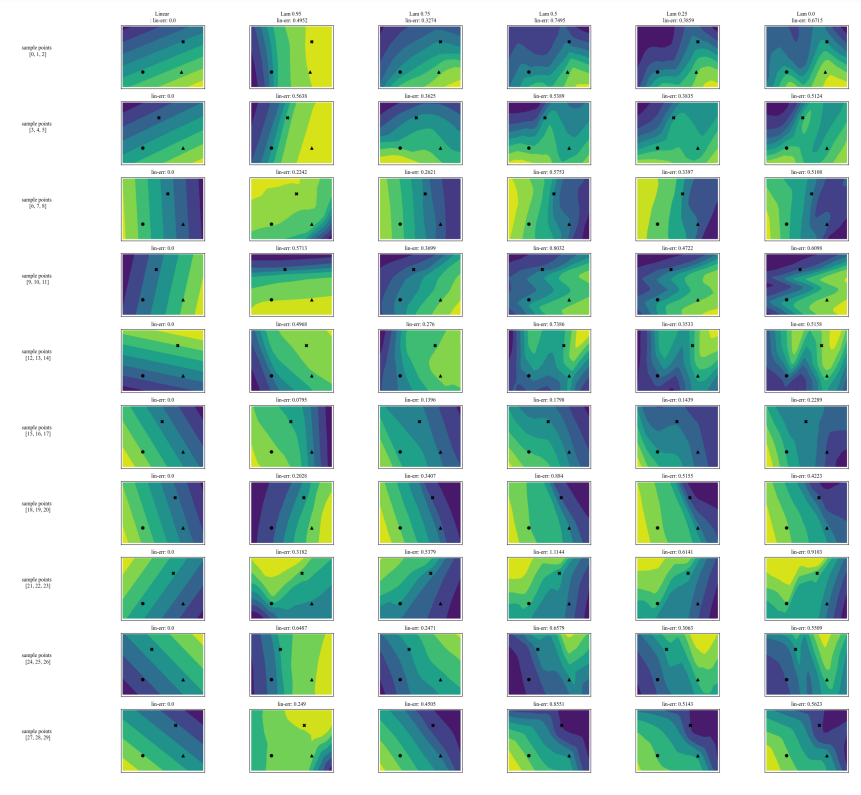
\ 圖13：MLP的logit曲面，每個都使用不同的lambda值訓練，在來自加州房價數據集的10個隨機構建的三點平面上。

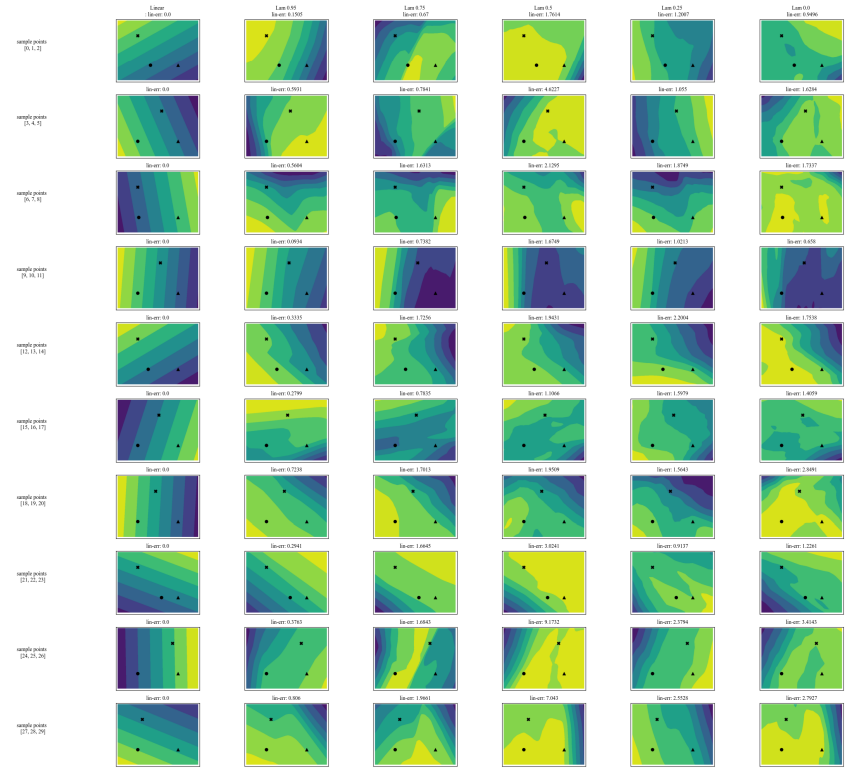
\ 圖14：MLP的logit曲面，每個都使用不同的lambda值訓練，在來自電力數據集的10個隨機構建的三點平面上。

\ 圖15：所有數據集和指標的額外權衡曲線圖。

:::info 作者：

(1) Avi Schwarzschild，馬里蘭大學，馬里蘭州學院公園，美國，以及在Arthur工作期間完成的工作(avi1umd.edu)；

(2) Max Cembalest，Arthur，紐約市，紐約州，美國；

(3) Karthik Rao，Arthur，紐約市，紐約州，美國；

(4) Keegan Hines，Arthur，紐約市，紐約州，美國；

(5) John Dickerson†，Arthur，紐約市，紐約州，美國(john@arthur.ai)。

:::

:::info 本論文可在arxiv上獲取，根據CC BY 4.0 DEED許可證。

:::

免責聲明: 本網站轉載的文章均來源於公開平台，僅供參考。這些文章不代表 MEXC 的觀點或意見。所有版權歸原作者所有。如果您認為任何轉載文章侵犯了第三方權利，請聯絡 service@support.mexc.com 以便將其刪除。MEXC 不對轉載文章的及時性、準確性或完整性作出任何陳述或保證，並且不對基於此類內容所採取的任何行動或決定承擔責任。轉載材料僅供參考，不構成任何商業、金融、法律和/或稅務決策的建議、認可或依據。