Research from Apple and EPFL Explains Why AI Models Can’t Truly “Reason” Yet

Table of Links

Abstract and 1. Introduction

1.1 Syllogisms composition

1.2 Hardness of long compositions

1.3 Hardness of global reasoning

1.4 Our contributions

1. Results on the local reasoning barrier

   2.1 Defining locality and auto-regressive locality

   2.2 Transformers require low locality: formal results

   2.3 Agnostic scratchpads cannot break the locality

2. Scratchpads to break the locality

   3.1 Educated scratchpad

   3.2 Inductive Scratchpads

3. Conclusion, Acknowledgments, and References

A. Further related literature

B. Additional experiments

C. Experiment and implementation details

D. Proof of Theorem 1

E. Comment on Lemma 1

F. Discussion on circuit complexity connections

G. More experiments with ChatGPT

D Proof of Theorem 1

\

\

\ At this point, we are finally ready to prove Theorem 1 as follows.

\

\

\

\

\

D.1 Extension to agnostic scratchpads

Theorem 1 can also be generalised to Transformers trained with agnostic scratchpads in order to get the following.

\ Theorem 2. Let G be a directed graph which consists of a cycle of length 3n with probability 2/3 and 3 cycles of length n otherwise. Next, if there are 3 cycles pick one vertex from each and if there is one cycle pick three vertices that are each n edges apart. Then, label uniformly at random these vertices with a0, b0, c0. Next, number every other vertex by the distance from one of these three to it, and for each i, label uniformly at random the vertices at distance i by ai, bi, and ci and store in X the edges between ai − 1, bi − 1, ci − 1 and ai, bi, ci; i.e.

\

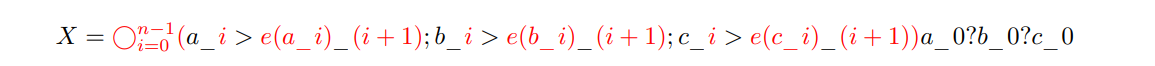
\ where e(v) represents the vertex that v’s edge points to, all of the instances of i or i + 1 should have the appropriate value substituted in and the symbols in black should be used exactly as stated. See Figure 2 for an example. Finally, let Y report whether a0, b0, c_0 are in the same cycle or not. Now, consider training a T-regular neural network with a scratchpad of polynomial length on (X, Y ) generated in this manner. For any given (X, Y ), we will regard the net’s loss on (X, Y ) as the expectation over all possible scratchpads that it might generate on X of the loss of its eventual output. If we train it on (X, Y ) using population[14] gradient descent with polynomial hyperparameters[15] and a differentiable loss function then the network fails to weakly learn to compute Y.

\ The proof of this theorem is not meaningfully different from the proof of the previous version, but for completeness we include it below.

\

\

\

\ That in turn means that

\

\

E Comment on Lemma 1

For S such that |S| < n, X[S] is independent of Y , since the distribution of such subsets of edges is the same for both classes.

\ Let S be such that |S| = n. Let ZS be the ternary random variable that records whether there is a cycle or an open path on S. Then,

\ Thus

\

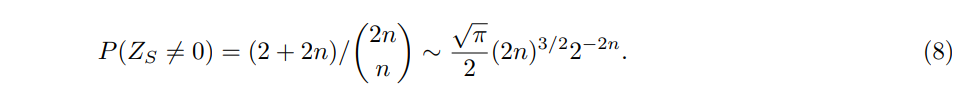
\ Therefore, even for sets of size n, the mutual information is exponentially low, implying that loc(D) is greater than n + 1

\

:::info Authors:

(1) Emmanuel Abbe, Apple and EPFL;

(2) Samy Bengio, Apple;

(3) Aryo Lotf, EPFL;

(4) Colin Sandon, EPFL;

(5) Omid Saremi, Apple.

:::

:::info This paper is available on arxiv under CC BY 4.0 license.

:::

[14] This would also be true for batch GD with batches of size n c with c chosen as a function of the other hyperparameters.

\ [15] I.e., either polynomial learning rate, polynomial clipping [12, 31], and weights stored using a logarithmic number of bits of precision and random rounding: for a < b < c if b needs to be rounded to a or c then it rounds to c with probability (b − a)/(c − a), or with polynomial learning rate, polynomial clipping and polynomial noise added to the gradients.