Understanding Training Stability in Hyperbolic Neural Networks
Table of Links
Abstract and 1. Introduction
-
Related Work
-
Methodology
3.1 Background
3.2 Riemannian Optimization
3.3 Towards Efficient Architectural Components
-
Experiments
4.1 Hierarchical Metric Learning Problem
4.2 Standard Classification Problem
-
Conclusion and References
3.1 Background
\
3.2 Riemannian Optimization
Optimizers for Learned Curvatures In their hyperbolic learning library GeoOpt, Kochurov et al. [21] attempt to make the curvature of the hyperbolic space a learnable parameter. However, we have found no further work that makes proper use of this feature. Additionally, our empirical tests show that this approach often results in higher levels of instability and performance degradation. We attribute these issues to the naive implementation of curvature updates, which fails to incorporate the updated hyperbolic operations into the learning algorithm. Specifically, Riemannian optimizers rely on Riemannian projections of Euclidean gradients and projected momentums onto the tangent spaces of gradient vectors. These operations depend on the current properties of the manifold that houses the hyperbolic parameters being updated. From this, we can identify one main issue with the naive curvature learning approach.
\ The order in which parameters are updated is crucial. Specifically, if the curvature of the space is updated before the hyperbolic parameters, the Riemannian projections and tangent projections of the gradients and momentums become invalid. This happens because the projection operations start using the new curvature value, even though the hyperbolic parameters, hyperbolic gradients, and momentums have not yet been reprojected onto the new manifold.
\ To resolve this issue, we propose a projection schema and an ordered parameter update process. To sequentialize the optimization of model parameters, we first update all manifold and Euclidean parameters, and then update the curvatures after. Next, we parallel transport all Riemannian gradients and project all hyperbolic parameters to the tangent space at the origin using the old curvature value. Since this tangent space remains invariant when the manifold curvature changes, we can assume the points now lie on the tangent space of the new origin as well. We then re-project the hyperbolic tensors back onto the manifold using the new curvature value and parallel transport the Riemannian gradients to their respective parameters. This process can be illustrated in algorithm 1.
\ 
\ Riemannian AdamW Optimizer Recent works, especially with transformers, rely on the AdamW optimizer proposed by Loshchilov and Hutter [26] for training. As of current, there is no established Riemannian variant of this optimizer. We attempt to derive AdamW for the Lorentz manifold and argue a similar approach could be generalized for the Poincaré ball. The main difference between AdamW and Adam is the direct weight regularization which is more difficult to perform in the Lorentz space given the lack of an intuitive subtraction operation on the manifold. To resolve this, we model the regularized parameter instead as a weighted centroid with the origin. The regularization schema becomes:
\ 
\ 
\ As such, we propose a maximum distance rescaling function on the tangent of the origin to conform with the representational capacity of hyperbolic manifolds.
\ 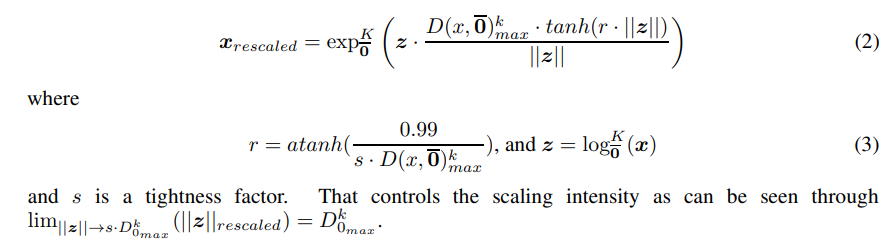
\ Specifically, we apply it when moving parameters across different manifolds. This includes moving from the Euclidean space to the Lorentz space and moving between Lorentz spaces of different curvatures. We also apply the scaling after Lorentz Boosts and direct Lorentz concatenations [31]. Additionally, we add this operation after the variance-based rescaling in the batchnorm layer. This is because we run into situations where adjusting to the variance pushes the points outside the radius during the operation.
3.3 Towards Efficient Architectural Components
Lorentz Convolutional Layer In their work, Bdeir et al. [1] relied on dissecting the convolution operation into a window-unfolding followed by a modified version of the Lorentz Linear layer by Chen et al. [3]. However, an alternative definition for the Lorentz Linear layer is offered by Dai et al. [5] based on a direct decomposition of the operation into a Lorentz boost and a Lorentz rotation. We follow the dissection scheme by Bdeir et al. [1] but rely on Dai et al. [5]s’ alternate definition of the Lorentz linear transformation. The core transition here would be moving from a matrix multiplication on the spatial dimensions followed by a reprojection, to learning an individual rotation operation and a Lorentz Boost.
\ 
\ out = LorentzBoost(TanhScaling(RotationConvolution(x)))
\ where TanhRescaling is the operation described in 2 and RotationConvolution is a normal convolution parameterized through the procedure in 2, where Orthogonalize is a Cayley transformation similar to [16]. We use the Cayley transformation in particular because it always results in an orthonormal matrix with a positive determinant which prevents the rotated point from being carried to the lower sheet of the hyperboloid.
\ Lorentz-Core Bottleneck Block In an effort to expand on the idea of hybrid hyperbolic encoders [1], we designed the Lorentz Core Bottleneck blocks for Hyperbolic Resnet-based models. This is similar to a standard Euclidean bottleneck block except we replace the internal 3x3 convolutional layer with our efficient convolutional layer as seen in figure 1. We are then able to benefit from a hyperbolic structuring of the embeddings in each block while maintaining the flexibility and speed of Euclidean models. We interpret this integration as a form of hyperbolic bias that can be adopted into Resnets without strict hyperbolic modeling.
Specifically, we apply it when moving parameters across different manifolds. This includes moving from the Euclidean space to the Lorentz space and moving between Lorentz spaces of different curvatures. We also apply the scaling after Lorentz Boosts and direct Lorentz concatenations [31]. Additionally, we add this operation after the variance-based rescaling in the batchnorm layer. This is because we run into situations where adjusting to the variance pushes the points outside the radius during the operation.
\
:::info Authors:
(1) Ahmad Bdeir, Data Science Department, University of Hildesheim (bdeira@uni-hildesheim.de);
(2) Niels Landwehr, Data Science Department, University of Hildesheim (landwehr@uni-hildesheim.de).
:::
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\
You May Also Like

BFX Presale Raises $7.5M as Solana Holds $243 and Avalanche Eyes $1B Treasury — Best Cryptos to Buy in 2025

US appeals court denies Custodia Bank rehearing in Fed case
