Shocks, Collisions, and Entropy—Neural Networks Handle It All
Table of Links
Abstract and 1. Introduction
1.1. Introductory remarks
1.2. Basics of neural networks
1.3. About the entropy of direct PINN methods
1.4. Organization of the paper
-
Non-diffusive neural network solver for one dimensional scalar HCLs
2.1. One shock wave
2.2. Arbitrary number of shock waves
2.3. Shock wave generation
2.4. Shock wave interaction
2.5. Non-diffusive neural network solver for one dimensional systems of CLs
2.6. Efficient initial wave decomposition
-
Gradient descent algorithm and efficient implementation
3.1. Classical gradient descent algorithm for HCLs
3.2. Gradient descent and domain decomposition methods
-
Numerics
4.1. Practical implementations
4.2. Basic tests and convergence for 1 and 2 shock wave problems
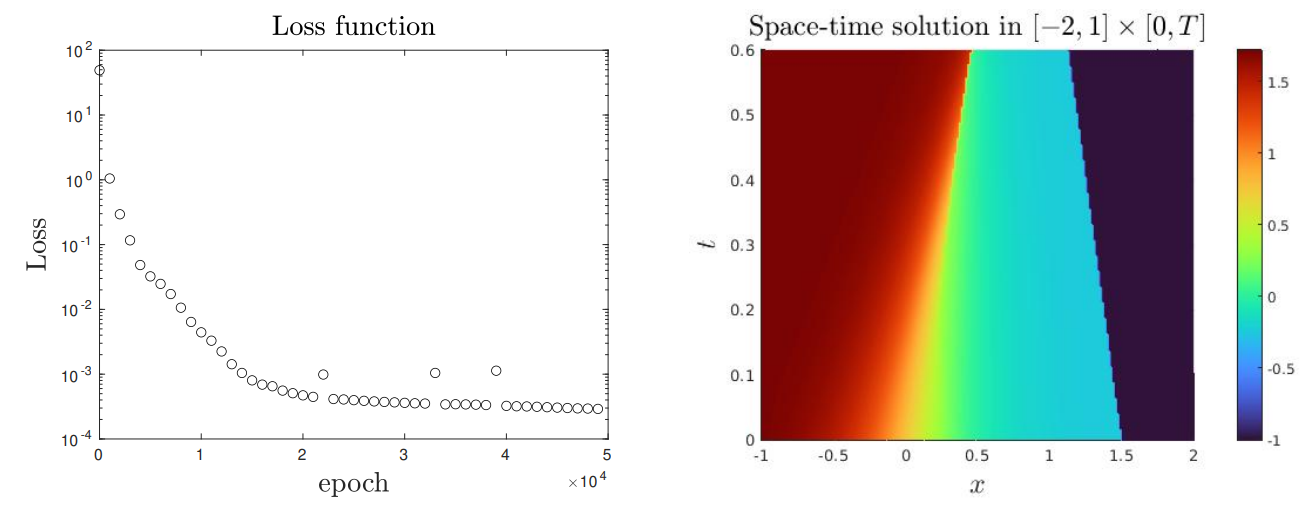
4.3. Shock wave generation
4.4. Shock-Shock interaction
4.5. Entropy solution
4.6. Domain decomposition
4.7. Nonlinear systems
-
Conclusion and References
4.3. Shock wave generation
In this section, we demonstrate the potential of our algorithms to handle shock wave generation, as described in Subsection 2.3. One of the strengths of the proposed algorithm
\ 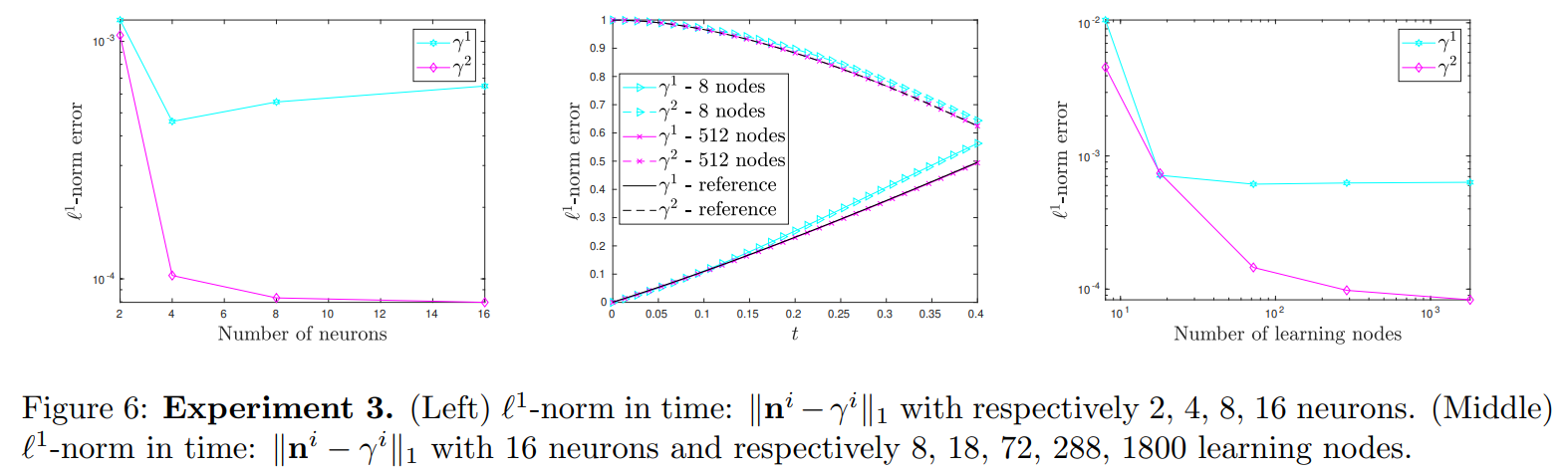
\ is that it does not require to know the initial position&time of birth, in order to accurately track the DLs. Recall that the principle is to assume that in a given (sub)domain and from a smooth function a shock wave will eventually be generated. Hence we decompose the corresponding (sub)domain in two subdomains and consider three neural networks: two neural networks will approximate the solution in each subdomain, and one neural network will approximate the DL. As long as the shock wave is not generated (say for t < t∗ ), the global solution remains smooth and the Rankine-Hugoniot condition is trivially satisfied (null jump); hence the DL for t < t∗ does not have any meaning.
\ Experiment 4. We again consider the inviscid Burgers’ equation, Ω × [0, T] = (−1, 2) × [0, 0.5] and the initial condition
\ 
\ 
\ 
\ 
\
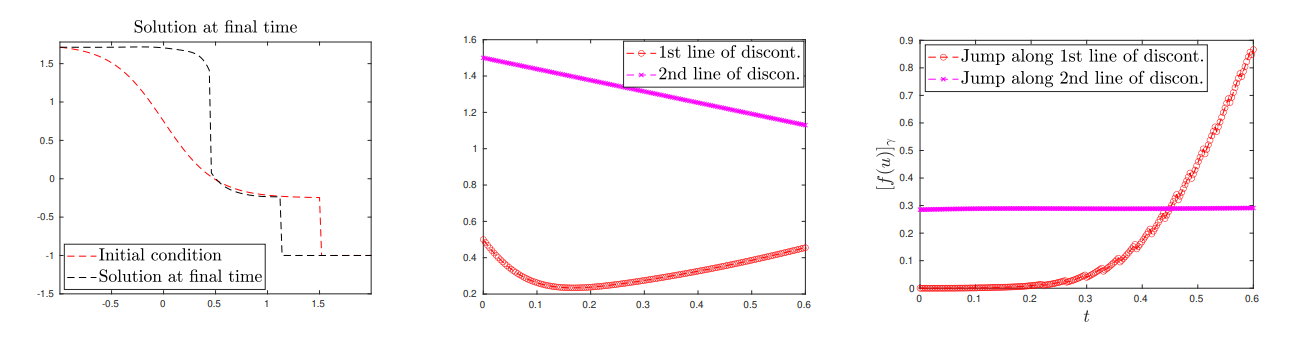
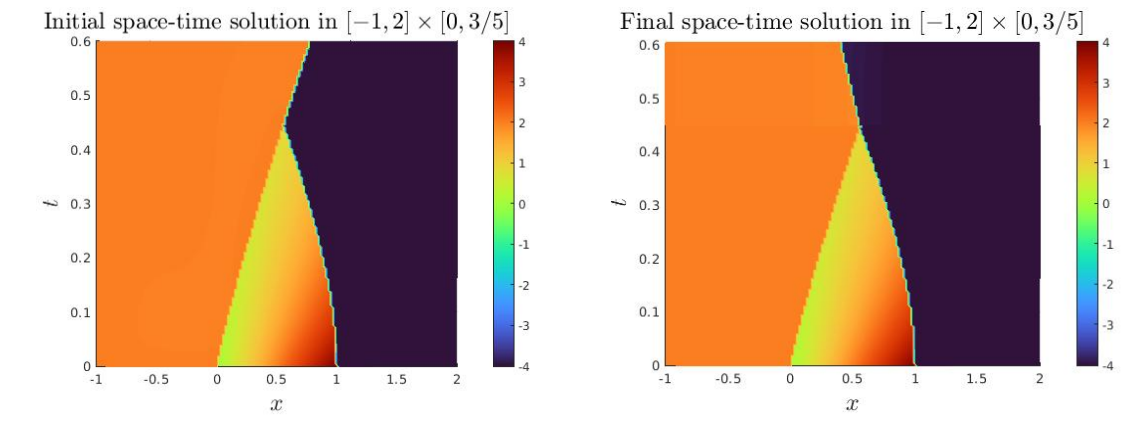
4.4. Shock-Shock interaction
In this subsection, we are proposing a test involving the interaction of two shock waves merging to generate a third shock wave. As explained in Subsection 2.4, in this case it is necessary re-decompose the full domain once the two shock waves have interacted.
\ \ 
\ \ \ 
\
4.5. Entropy solution
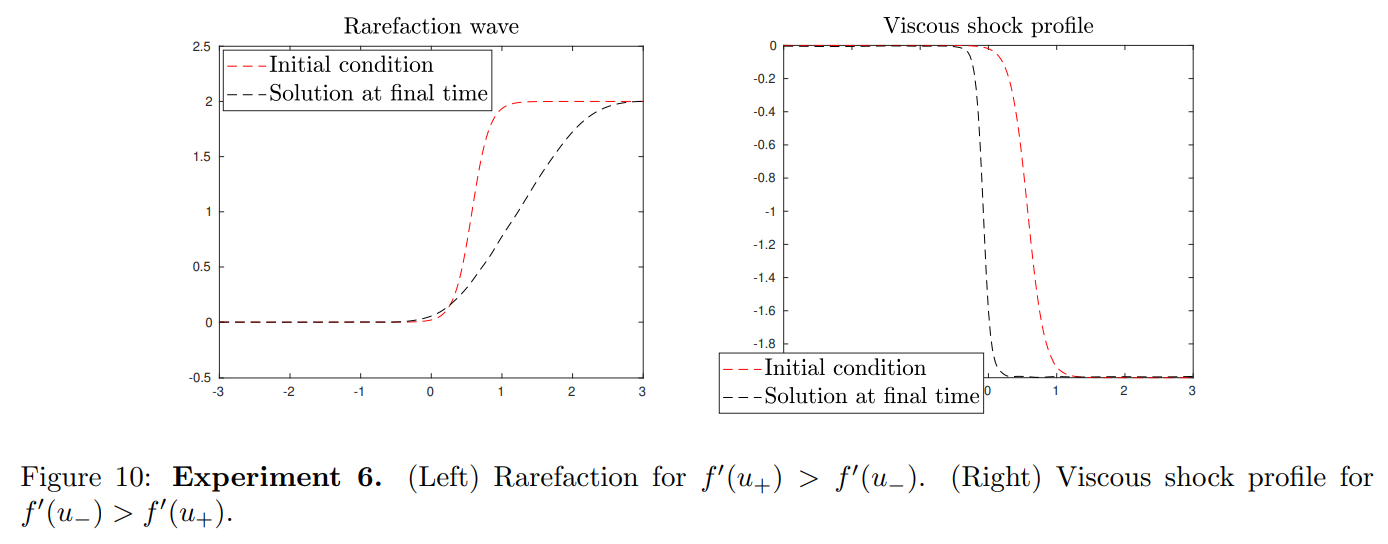
We propose here an experiment dedicated to the computation of the viscous shock profiles and rarefaction waves and illustrating the discussion from Subsection 1.3. In this example, a regularized non-entropic shock is shown to be “destabilized” into rarefaction wave by the direct PINN method.
\ \ 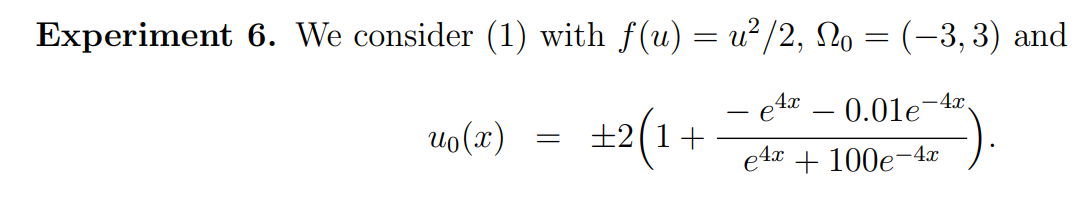
\ \ \ \ 
\ \ \ 
\ \
:::info Authors:
(1) Emmanuel LORIN, School of Mathematics and Statistics, Carleton University, Ottawa, Canada, K1S 5B6 and Centre de Recherches Mathematiques, Universit´e de Montr´eal, Montreal, Canada, H3T 1J4 (elorin@math.carleton.ca);
(2) Arian NOVRUZI, a Corresponding Author from Department of Mathematics and Statistics, University of Ottawa, Ottawa, ON K1N 6N5, Canada (novruzi@uottawa.ca).
:::
:::info This paper is available on arxiv under CC by 4.0 Deed (Attribution 4.0 International) license.
:::
\
You May Also Like

Gold price in Saudi Arabia: Rates on December 15

Little Pepe soars from presale to market spotlight
