Comprendre l'erreur d'approximation et la complexité des requêtes dans le routage WormHole

Table des Liens

Abstrait et 1. Introduction

1.1 Notre Contribution

1.2 Cadre

1.3 L'algorithme

1. Travaux Connexes

2. Algorithme

   3.1 La Phase de Décomposition Structurelle

   3.2 La Phase de Routage

   3.3 Variantes de WormHole

3. Analyse Théorique

   4.1 Préliminaires

   4.2 Sous-linéarité de l'Anneau Intérieur

   4.3 Erreur d'Approximation

   4.4 Complexité des Requêtes

4. Résultats Expérimentaux

   5.1 WormHole𝐸, WormHole𝐻 et BiBFS

   5.2 Comparaison avec les méthodes basées sur l'indexation

   5.3 WormHole comme primitive: WormHole𝑀

Références

4.3 Erreur d'Approximation

Maintenant que nous avons un anneau intérieur sous-linéaire qui contient le noyau de Chung-Lu, nous devons montrer que le routage des chemins à travers celui-ci n'entraîne qu'une petite pénalité. Intuitivement, plus l'anneau intérieur est grand, plus il est facile de satisfaire cette condition : si l'anneau intérieur est le graphe entier, l'affirmation est trivialement vraie. Par conséquent, le défi consiste à montrer que nous pouvons obtenir une forte garantie en termes de précision même avec un anneau intérieur sous-linéaire. Nous prouvons que WormHole entraîne une erreur additive d'au plus 𝑂(loglog𝑛) pour toutes les paires, ce qui est beaucoup plus petit que le diamètre Θ(log𝑛).

\

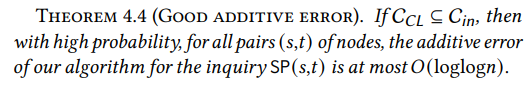
\ Le résultat ci-dessus est valable avec une forte probabilité même dans le pire des cas. À savoir, pour toutes les paires (𝑠,𝑡) de sommets dans le graphe, la longueur du chemin renvoyé par WormHole est au plus 𝑂(loglog𝑛) plus élevée que la distance réelle entre 𝑠 et 𝑡. Cela implique trivialement que l'erreur additive moyenne de WormHole est, avec une forte probabilité, limitée par la même quantité.

\

\

4.4 Complexité des Requêtes

Rappelons le modèle de requête de nœud dans cet article (voir §1.2) : en partant d'un seul nœud, nous sommes autorisés à faire des requêtes de manière itérative, où chaque requête récupère la liste des voisins d'un nœud 𝑣 de notre choix. Nous nous intéressons à la complexité des requêtes, c'est-à-dire au nombre de requêtes nécessaires pour effectuer certaines opérations.

\ \

\ \ Le premier résultat est la borne supérieure de notre performance.

\ \

\ \ Esquisse de preuve. Pour une requête donnée SP(𝑢, 𝑣), nous donnons une borne supérieure sur la complexité des requêtes du BFS qui commence à 𝑢, et de même pour 𝑣 ; la complexité totale des requêtes est la somme de ces deux quantités.

\ \

\ \ \

\ \ \

\ \ \

\ \ \

\ \

:::info Auteurs :

(1) Talya Eden, Université Bar-Ilan (talyaa01@gmail.com) ;

(2) Omri Ben-Eliezer, MIT (omrib@mit.edu) ;

(3) C. Seshadhri, UC Santa Cruz (sesh@ucsc.edu).

:::

:::info Cet article est disponible sur arxiv sous licence CC BY 4.0.

:::

\